Determining Order of Reaction and Rate Law Tutorial

Key Concepts

The order with respect to one species in the reaction is the exponent on the concentration term for that species in the rate law.
For the rate law: rate = k[A][B]²

For Species: Exponent of
concentration Rate is

A 1 first order

B 2 second order

The order of a reaction is the sum of the exponents on the concentration terms in the rate law.
For the rate law: rate = k[A][B]²

order of reaction = exponent of [A] + exponent of [B]
order of reaction = 1 + 2 = 3
Reaction is third order.

Several methods can be used to determine the rate law from experimental data.
The three most common methods are :

For Species:	Exponent of concentration	Rate is
A	1	first order
B	2	second order

(i)	Initial Rate Method	Several experiments are run at the same temperature, the rate at the start of each experiment is determined, then the results of all the experiments analyzed to determine the relationship between initial concentration and initial rate. Zero order reaction: rate is independent of the concentration of the species First order reaction: rate ∝ [species] Second order reaction: rate ∝ [species]²
(ii)	Graphical Method	First order reaction: A plot of log₁₀[species] against time produces a straight line. The slope of the line = -k/2.303 Second order reaction: A plot of 1/[species] against time produces a straight line. The slope of the line = k
(iii)	Half-Life Method ¹	Let: [A]₀ = the initial concentration of species A k = specific rate constant for the reaction t = sometime later on in the experiment [A]_t = the concentration of A at time t Then we find that there is an exponential relationship between the concentration of A and the length of time the experiment is allowed to run for: [A]_t = [A]₀ × e^-kt So, by rearranging this equation we find that: [A]/[A]₀ = e^-kt Taking the natural logarithm (ln) of both sides of the equation we get: ln([A]/[A]₀) = -kt or, by converting natural logarithms (ln) to logarithms to the base to (log₁₀) we find that: log₁₀[A] = -kt/2.303 + log[A]₀ Half-life, t_½, is the time taken for half the quantity of a reactant to be consumed, so log[A]_½ = -kt_½/2.303 + log[A]₀ First order reaction: Half-life of a first order reaction is a constant, ie, half-life is independent of initial concentration. First order reaction: t_½ = 0.693/k Second order reaction: Half-life of a second order reaction is not independent of intial concentration. For the second order reaction: A → B where rate = k[A]² t_½ = 1/k[A]

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Examples of Initial Concentration Method to Determine Rate Law

Question 1 : Determining the Rate Law of a Zero Order Reaction

Ammonia, NH_3(g), can be decomposed on the surface of tungsten metal to produce nitrogen, N_2(g), and hydrogen, H_2(g), according to the equation:

2NH_3(g) → 3H_2(g) + N_2(g)

The results of a series of experiments carried out at the same temperature are shown below:

Trial	Initial [NH₃] (M)	Initial Rate (M/min)
1	2.50 × 10^-3	6.67 × 10^-7
2	5.00 × 10^-3	6.67 × 10^-7

Determine the rate law for this reaction.

Solution:

Determine the change in initial concentration:
The initial concentration of NH₃ was increased by a factor of

[NH_{3(trial 2)}]
[NH_{3(trial 1)}] = 5.00 × 10^-3
2.50 × 10^-3 = 2

Determine the change in initial rate as a result of this change in concentration:
The initial rate of the reaction increased by a factor of

rate_{(trial 2)}
rate_{(trial 1)} = 6.67 × 10^-7
6.67 × 10^-7 = 1

That is, the rate does NOT change when the concentration of NH₃ changes.

Determine the relationship between the change in concentration and the change in rate:
Since increasing the concentration by a factor of 2 leads to no increase in the rate, the reaction rate is independent of the concentration of NH₃
rate = k

The reaction is zero order.

Calculate the specific rate constant, k, for the reaction:

k = rate

Using data from Trial 1:
k = 6.67 × 10^-7

Write the rate law for this reaction:
rate = 6.67 × 10^-7

Question 2: Determining the Rate Law of a First Order Reaction

Azomethane, C₂H₆N₂, decomposes to produce ethane, C₂H₆, and nitrogen, N₂.

C₂H₆N_2(g) → C₂H_6(g) + N_2(g)

The results of a series of experiments carried out at the same temperature are shown below:

Trial	Initial [C₂H₆N_2(g)] (M)	Initial Rate (M/min)
1	2.00 × 10^-2	3.00 × 10^-4
2	4.00 × 10^-2	6.00 × 10^-4

Determine the rate law for this reaction.

Solution:

Determine the change in initial concentration:
The initial concentration of C₂H₆N_2(g) was increased by a factor of

[C₂H₆N_{2(g)(trial 2)}]
[C₂H₆N_{2(g)(trial 1)}] = 4.00 × 10^-2
2.00 × 10^-2 = 2

Determine the change in initial rate as a result of this change in concentration:
The initial rate of the reaction increased by a factor of

rate_{(trial 2)}
rate_{(trial 1)} = 6.00 × 10^-4
3.00 × 10^-4 = 2

Determine the relationship between the change in concentration and the change in rate:
Since increasing the concentration by a factor of 2 leads to an increase in the rate by a factor of 2, the reaction rate and the concentration of C₂H₆N_2(g) are directly proportional:
rate ∝ [C₂H₆N_2(g)]

So, rate = k[C₂H₆N_2(g)]

The reaction is first order.

Calculate the specific rate constant, k, for the reaction:

k = rate
[C₂H₆N_2(g)]

Using data from Trial 1:

k = 3.00 × 10^-4
2.00 × 10^-2 = 0.015

Write the rate law for this reaction:
rate = 0.015[C₂H₆N_2(g)]

Question 3: Determining the Rate Law of a Second Order Reaction

Hydrogen iodide decomposes to hydrogen and iodine according to the equation:

2HI → H₂ + I₂

The results of a series of experiments carried out at the same temperature are shown below:

Trial	Initial [HI] (M)	Intial Rate (M/min)
1	1.50 × 10^-3	1.20 × 10^-5
2	3.00 × 10^-3	4.8 × 10^-5

Determine the rate law for this reaction.

Solution:

Determine the change in initial concentration:
The initial concentration of HI was increased by a factor of

[HI_{2(g)(trial 2)}]
[HI_{2(g)(trial 1)}] = 3.00 × 10^-3
1.50 × 10^-3 = 2

Determine the change in initial rate as a result of this change in concentration:
The initial rate of the reaction increased by a factor of

rate_{(trial 2)}
rate_{(trial 1)} = 4.8 × 10^-5
1.20 × 10^-5 = 4 = 2²

Determine the relationship between the change in concentration and the change in rate:
Since increasing the concentration of HI by a factor of 2 leads to an increase in the rate by a factor of 2², the rate is proportional to the square of the concentration of HI,
rate ∝ [HI]²

So, rate = k[HI]²

The reaction is second order.

Calculate the specific rate constant, k, for the reaction:

k = rate/[HI]²

Using data from Trial 1:

k = 1.20 × 10^-5
[1.50 × 10^-3]² = 1.20 × 10^-5
2.25 × 10^-6 = 5.33
Write the rate law for this reaction:
rate = 5.33[HI]²

Do you know this?

Join AUS-e-TUTE!

Do the drill now!

Examples of Graphical Method for Determining Rate Law

Question 1: Determining the Rate Law of a First Order Reaction

The decomposition of gaseous dinitrogen pentoxide, N₂O₅, was investigated at a particular temperature.

The results of the experiment are shown below:

Time (min)	0.00	5.00	10.00	15.00	20.00	25.00
[N₂O₅] (M)	1.30	1.08	0.90	0.75	0.62	0.52

Show that the reaction is first order and determine the rate law for this reaction.

Solution:

Calculate log₁₀[N₂O₅]

Time (min)	0.00	5.00	10.00	15.00	20.00	25.00
[N₂O₅] (M)	1.30	1.08	0.90	0.75	0.62	0.52
log₁₀[N₂O₅]	0.11	0.03	-0.05	-0.12	-0.21	-0.28

Plot log₁₀[N₂O₅] against time (shown below)

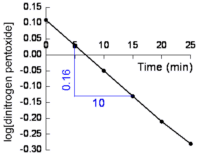
Straight line graph means the reaction is first order.

Rate is directly proportional to N₂O₅ concentration.

rate ∝ [N₂O₅]

rate = k[N₂O₅]

Calculate the slope of the line:

from the graph (shown in blue):

slope =

-0.16
10.00

= -0.016

mathematically:

slope =	y₁ - y₂ x₁ - x₂
=	0.11 - (-0.28) 0.00 - 25.00
=	0.39 -25.00
=	-0.016

Calculate the specific rate constant, k, for this reaction:

slope	=	-k 2.303
2.303 × slope	=	-k
-2.303 × slope	=	k

Substitute the value for the slope into the equation and solve to find the specific rate constant, k

k = -slope × 2.303

= -(-0.016) × 2.303

= 0.037

Write the rate law for this reaction:
rate = 0.037[N₂O₅]

Question 2: Determining the Rate Law of a Second Order Reaction

An investigation into the decomposition of NO₂ at a particular temperature produced the following results:

Time (s)	0.00	5.00	10.00	15.00	20.00
[NO₂] (M)	0.10	0.017	0.0089	0.0062	0.0047

Use the data to verify that that reaction is second order and determine the rate law for the reaction.

Solution:

Calculate the reciprocal concentrations of NO₂

Time (s)	0.00	5.00	10.00	15.00	20.00
[NO₂] (M)	0.10	0.017	0.0089	0.0062	0.0047
1/[NO₂]	10	59	112	161	213

Plot 1/[NO₂] against time (shown below):

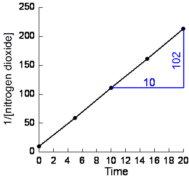
Straight line graph means the reaction is second order.

rate is proportional to the square of the concentration

rate ∝ [NO₂]²

rate = k[NO₂]²

Calculate the slope of the line:

from the graph (shown in blue):

slope =

102
10

= 10.2

mathematically:

slope =	(y₁ - y₂) (x₁ - x₂)
=	(10 - 213) (0 - 20)
=	-203 -20
=	10.2

Calculate the specific rate constant, k, for this reaction:
slope = k = 10.2

Write the rate law for this reaction:
rate = 10.2[NO₂]²

Do you understand this?

Join AUS-e-TUTE!

Do the drill now!

Examples of Half-Life Method for Determining Rate Law

Question 1: Using a Graph to Determine Half-Life

The results of the decomposition of gaseous dinitrogen pentoxide, N₂O₅, at various times are tabulated below.

Time (min)	0.00	10	20	30	40	50	60
[N₂O₅] (M)	348.8	247	185	140	105	78	58

Use the data to confirm that this reaction is first order and find the specific rate constant at this temperature.

Solution:

Plot [N₂O₅] against time as shown below:

Use the graph to obtain half-life values:

[N₂O₅]₀ (M)	Graph Reference	t_½ (min)
300	a to b	24
250	c to d	24
200	e to f	24
150	b to g	24

Half-life is independent of [N₂O₅]₀ so the reaction is first order.
That is, as [N₂O₅]₀ changes, the half-life, t_½ is constant

Calculate the specific rate constant, k.

For a first order reaction:

t_½	=	0.693 k
k	=	0.693 t_½
	=	0.693 24
	=	0.029

Question 2: Using the Exponential Equation to Determine Half-Life

The decomposition of gaseous N₂O₃ to form NO₂ and NO is first order with k = 3.2 × 10^-4s^-1.

If the initial concentration of N₂O₃ is 1.00 M, how long will it take for its concentration to be decreased to 0.125 M ?

Solution:

The relationship between concentration and time is :

log₁₀[A]_t = -kt
2.303 + log₁₀[A]₀

Extract the data from the question:
[N₂O₃]₀ = 1.00 M

[N₂O₃]_t = 0.125 M

k = 3.2 × 10^-4s^-1

t = ?

Substitute the values into the equation:

log₁₀[A]_t	=	-kt 2.303	+ log₁₀[A]₀
log₁₀[0.125]	=	-3.2 x 10^-4t 2.303	+ log₁₀[1.00]
-0.903	=	-3.2 x 10^-4t 2.303	+ 0
-0.903 × 2.303 -3.2 x 10^-4	=	t
6499 s	=	t

Alternatively:

[N₂O₃]_t	=	[N₂O₃]₀e^-kt
ln( [N₂O₃]_t ) [N₂O₃]₀	=	-kt
ln([N₂O₃]_t/[N₂O₃]₀ -k	=	t
ln(0.125/1.00) -(-3.2 × 10^-4)	=	t
6498 s	=	t

Alternatively:

Recognize that the time for 1.00 M to reduce to 0.125 M is equivalent to 3 half-lives:

Time	[N₂O₃]
0	1.00
1 half-life	0.500 M
2 half-lives	0.250 M
3 half-lives	0.125 M

For a first order reaction:

t_½	=	0.693 k
	=	0.693 3.2 × 10^-4
	=	2166 s

3 half-lives = 3 × 2166 = 6498 s

Can you apply this?

Join AUS-e-TUTE!

Do the drill now!

1. If you are looking for information about radioactive half-life, go to the Half-life Tutorial