Kinetic Energy Distribution Concepts for Understanding Reaction Rate Tutorial

Key Concepts

• At a particular temperature, molecules display a range of kinetic energies, known as the Maxwell-Boltzmann distribution.

• The area under the kinetic energy (Maxwell-Boltzmann) distribution curve represents the number of molecules within a given range of kinetic energies:

  ⚛ Small area under curve = small number of molecules.

  ⚛ Large area under curve = large number of molecules.

• Increasing the temperature from T₁ to T₂ causes the kinetic energy (Maxwell-Boltzmann) distribution curve to shift toward higher kinetic energy.

  

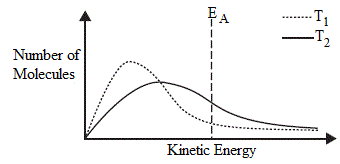
• The activation energy, E_A, is the minimum amount of energy reactant molecules must possess in order to successfully collide to produce products.
• At the higher temperature, T₂:

  (a) area under T₂ curve to the right of E_A is greater than the area under T₁ curve to right of E_A

  (b) at T₂ more molecules possess energy greater than E_A, compared to T₁

  (c) reaction is faster at higher temperature, T₂, than at lower temperature, T₁

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Kinetic Energy Distribution Concepts

The kinetic energy of individual N_2(g) molecules¹ at 273 K (0°C) in a closed vessel was measured in an experiment.
The number of N_2(g) molecules with the same kinetic energy was recorded. The results are shown in the table below:

These results were then plotted on a graph as shown below:

Notice that all the molecules do not have the same kinetic energy at the same temperature (273 K).
The molecules show a distribution of kinetic energies at the same temperature.

Consider the number of molecules with low kinetic energy, for example, kinetic energy less that 100 × 10^-3 J.

We can see that the orange area in the bar graph represents the number of molecules with kinetic energy less than 100 × 10^-3 J and the blue area in the bar graph represents the number of molecules with kinetic energy greater than 100 × 10^-3 J.

The kinetic energy distribution of molecules at a particular temperature can be calculated using equations derived by James Clerk Maxwell and Ludwig Boltzmann in the nineteenth century³.
For this reason, the kinetic energy distribution is referred to as the Maxwell-Boltzmann distribution.

The Maxwell-Boltzmann distribution for our N_2(g) molecules at 273 K is shown below:

The solid orange line in the graph is the calculated kinetic energy distribution curve.

The shaded orange area under the curve represents the total number of molecules in the sample.

Activation Energy and Rates of Reaction Using the Maxwell-Boltzmann Distribution Curve

Activation energy refers to the minimum amount of energy reactant molecules need in order for a successful collision to take place, that is, for a collision that results in a chemical reaction.

Consider a reaction involving N_2(g) in which the activation energy is low, for example 200 × 10^-3 J.

We can show this activation energy on our graph of the Maxwell-Boltzmann distribution for N_2(g) molecules at 273 K as shown below:

The graph clearly shows that the orange area under the curve representing the number of molecules with kinetic energy less than 200 × 10^-3 J is very much smaller than the blue area under the curve representing the number of molecules with kinetic energy greater than 200 × 10^-3 J.

Most of the N_2(g) molecules have kinetic energy greater than 200 × 10^-3 J.
Since the activation energy for this reaction is 200 × 10^-3 J, most of the N_2(g) molecules have more than the required energy for successful collisions.
We expect this reaction to take place rapidly at this temperature (273 K).

Now consider a different reaction involving N_2(g) in which the activation energy is high, for example 1250 × 10^-3 J.

We can represent this much higher activation energy on the same Maxwell-Boltzmann (kinetic energy) distribution for our N_2(g) molecules at 273 K as shown below:

The graph clearly shows that the orange area under the curve representing the number of molecules with kinetic energy less than 1250 × 10^-3 J is very much larger than the blue area under the curve representing the number of molecules with kinetic energy greater than 1250 × 10^-3 J.

Few of the N_2(g) molecules have kinetic energy greater than 1250 × 10^-3 J.
Since the activation energy for this reaction is 1250 × 10^-3 J, most of the N_2(g) molecules have less than the required energy for successful collisions.
We expect this reaction to take place slowly at this temperature.

Effect of Temperature on the Maxwell-Boltzmann Distribution Curve

If the sample of N_2(g) is heated, then the molecules are expected to move faster, that is, the molecules gain kinetic energy.

The original sample of N_2(g) molecules at 273 K (0°C) used above is now heated to 1273 K (1000°C).
The number of N_2(g) molecules with the same kinetic energy was recorded, and then graphed as shown below:

Increasing the temperature from 273 K to 1273 K causes a general shift of the kinetic energy distribution for the molecules toward higher kinetic energy.

At the higher temperature, the distribution of kinetic energies of the molecules results in a curve that is broader (less peaked) than the distribution curve at the lower temperature.
At the higher temperature, the molecules display a greater spread (or range) of kinetic energy.

Effect of Temperature on Rate of Reaction Using Maxwell-Boltzmann Distribution Curve

Consider the reaction involving N_2(g) discussed above for which the activation energy was 1250 × 10^-3 J.

The activation energy for the reaction, the minimum amount of energy the molecules require in order to collide successfully to produce products, does not change with an increase in temperature, but the kinetic energy each molecule possesses does change with temperature as seen above.

The kinetic energy (Maxwell-Boltzmann) distribution curve for N_2(g) molecules at 273 K and 1273 K is plotted and the activation energy (1250 × 10^-3 J) is shown in the graph below.

Remember that the area under each curve represents the number of molecules within a given range of kinetic energies.

Let us compare the area under each curve on our graph for the range of kinetic energies between the activation energy and 14000 x 10^-3 J in order to describe the relative rate of the reaction at each temperature:

More of the molecules have a kinetic energy greater than the activation energy for the reaction at the higher temperature, so the reaction proceeds more rapidly at the higher temperature.