Hess's Law of Constant Heat Summation Chemistry Tutorial
Key Concepts
⚛ Hess's law of constant heat summation is more commonly known as Hess's law.
⚛ Hess's Law states that the change in enthalpy for any reaction depends only on the nature of the reactants and products and is independent of the number of steps or the pathway taken between them.
⚛ Different reaction pathways can be represented on the same energy diagram to represent the application of Hess's Law.
⚛ Hess's Law can be used to calculate the overall enthalpy change for a chemical reaction, ΔrH(overall), the enthalpy changes for each individual reaction during the process are added together (that is, summed).(1)
ΔrH(overall) = ΔrH(reaction 1) + ΔrH(reaction 2) + ...
⚛ Steps involved in calculating enthalpy change for a reaction, ΔrH(overall), using Hess's Law:
Step 1: Rearrange each equation so that it is balanced, with the reactants and products on the correct side.
Check that you have the correct states, enthalpy changes will be different for species in the solid, liquid and gas states.
Step 2: Assign each rearranged equation the correct ΔrH value.
Remember, if you need to multiply each species in the chemical equation by 2, then the enthalpy change must also be multiplied by 2.
If you reverse a chemical equation, then the sign of the enthalpy term also changes.
Step 3: Add the rearrranged equations together to give the overall equation for the reaction.
Step 4: Add the ΔrH values for these equations to calculate ΔrH for the overall reaction.
Please do not block ads on this website.
No ads = no money for us = no free stuff for you!
Understanding Hess's Law of Constant Heat Summation
If you want to walk from the bottom of a steep hill to the top of the hill, you have a couple of choices:
(i) the direct route: walk in a straight line from bottom to top.
(ii) the indirect route: walk in a spiral around the hill from bottom to top.
Either route will provide the desired result of arriving at the top of the hill.
The first route is the shortest route be it will be very tiring because of the steep gradient.
The second route is a longer route but will be less tiring because you are reducing the gradient as you travel.
Your potential energy at the bottom of the hill is less than your potential energy at the top of the hill, and this does NOT depend on the path you choose to travel.
Therefore, your overall change in potential energy is the same irrespective of which path you choose to walk.
Chemical reactions can be considered in just the same way.
The reactants in a chemical reaction have a certain chemical potential energy or enthalpy, H.
The products in a chemical reaction have a certain chemical potential energy or enthalpy, H.
The overal change in chemical potential energy that occurs when reactants are converted to products, ΔH, does NOT depend on the path the chemical reaction follows, it only depends on the nature of the reactants and products.
Consider the combustion, or burning in oxygen gas, of coal (solid carbon, C(s)).
There are a couple of different routes, or pathways, that could be used to produce carbon dioxide gas as the product of the reaction:
(i) The direct route: combust the carbon using excess oxygen gas
C(s) + O2(g) → CO2(g)
This reaction releases 393.5 kJ of energy per mole of CO2(g) produced. (2)
C(s) + O2(g) → CO2(g) ΔcH(C(s)) = -393.5 kJ mol-1
(ii) The less direct route: first convert the carbon to carbon monoxide, then react this carbon monoxide with oxygen to produce carbon dioxide:
Reaction 1: Combust carbon in a limited supply of oxygen gas so that carbon monoxide is produced:
C(s) + ½O2(g) → CO(g)
This reaction releases 110.5 kJ of energy per mole of CO(g) produced.
C(s) + ½O2(g) → CO(g) ΔrH(reaction 1) = -110.5 kJ mol-1
Reaction2: Combust all of this carbon monoxide in additonal oxygen to produce carbon dioxide gas:
CO(g) + ½O2(g) → CO2(g)
This reaction releases 283 kJ of energy per mole of CO(g) consumed, or, per mole of CO2(g) produced.
CO(g) + ½O2(g) → CO2(g) ΔrH(reaction 2) = -283 kJ mol-1
The big question is whether these two different reaction pathways, direct and indirect, are the same or different in terms of the overall chemical equation and enthalpy change.
First we can check to see if the overall chemical equations for the two reaction pathways is the same by adding together the chemical reactions for reaction 1 and reaction 2 in the indirect pathway.
I can represent this two-step process as in the diagram below:
| C(s) + ½O2(g) |
→ |
CO(g) |
| |
|
+ |
| |
|
½O2(g) |
| |
|
↓ |
| |
|
CO2(g) |
The combustion of 1 mole of C(s) used ½ mole of O2(g) to produce 1 mole of CO(g), BUT, all of this CO(g) is then combusted using another ½ mole O2(g) to produce 1 mole of CO2(g).
Overall the reaction combusted 1 mole of C(s) using 2 × ½ = 1 mole of O2(g), to produce 1 - 1 = 0 moles of CO(g), and, 1 mole of CO2(g).
In other words:
C(s) + O2(g) → CO2(g)
So, this two-step indirect method results in the same overall chemical equation as the direct one-step approach.
But, which reaction pathway, direct or indirect, produces the most energy per mole of CO2(g) produced?
(i) Direct route produces 393.5 kJ of energy per mole of CO2(g) produced:
C(s) + O2(g) → CO2(g) ΔcH(C(s)) = -393.5 kJ mol-1
(ii) Indirect route:
First reaction produces 110.5 kJ of energy per mole of C(s) combusted.
C(s) + ½O2(g) → CO(g) ΔrH(reaction 1) = -110.5 kJ mol-1
Second reaction produces 283 kJ of energy per mole of CO(g) combusted.
CO(g) + ½O2(g) → CO2(g) ΔrH(reaction 2) = -283 kJ mol-1
Total amount of energy released by indirect pathway = 110.5 + 283 = 393.5 kJ mol-1
Overall reaction: C(s) + O2(g) → CO2(g) ΔrH(overall) = -393.5 kJ mol-1
We can now see that the combustion of carbon via the direct 1-step pathway, or, via the indirect 2-step pathway, results in the same CO2(g) product, AND, releases exactly the same amount of energy per mole of CO2(g) produced.
This is what Hess's Law of Constant Heat Summation means for this reaction, the enthalpy change for the reaction in which carbon and oxygen gas react to produce carbon dioxide gas is the same, or constant, for the two different pathways we could use.
↪ Back to top
Representing and Using Hess's Law of Constant Heat Summation
Chemists often use a diagram to show the different pathways for the same overall chemical reaction, and, the enthalpy changes associated with each pathway.
The diagram below represents the combustion of carbon in oxygen to produce carbon dioxide by the two pathways described in the previous section, the direct 1-step pathway and the indirect 2-step pathway:
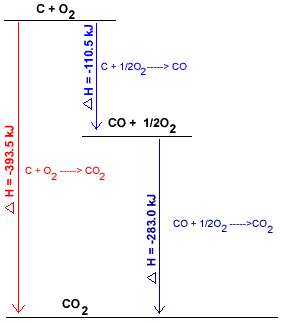
Direct Path
(1-step pathway) |
Indirect Path
(2-step pathway) |
|---|
|
C(s) + O2(g) → CO2(g)
393 kJ mol-1 of energy released, energy is a product of the reaction:
C(s) + O2(g) → 393 kJ mol-1 + CO2(g)
The reactants, C(s) and O2(g), are of higher enthalpy than the product, CO2(g)
C(s) and O2(g) are placed at the top of the diagram, CO2(g) is placed at the bottom of the diagram.
The arrow shows which direction the reaction is going (from C + O2 to CO2(g))
|
(i) C(s) + ½O2(g) → CO(g)
110.5 kJ mol-1 of energy is released, energy is a product.
C(s) + ½O2(g) → 110.5 kJ mol-1 + CO(g)
C(s) and O2(g) have higher enthalpy than CO(g) and are placed at the top of the diagram.
(ii) CO(g) + ½O2(g) → CO2(g)
283 kJ mol-1 of energy is released, energy is a product.
CO(g) + ½O2(g) → 283 kJ mol-1 + CO2(g)
CO(g) and O2(g) have higher enthalpy than CO2(g) so are placed above CO2(g) in the diagram.
|
Usually, we treat Hess's Law of Constant Heat Summation like a set of simultaneous equations in mathematics when we use it to calculate the enthalpy change for an "overall chemical reaction" resulting from multiple reaction pathways.
For the indirect 2-step pathway for the production of CO2(g) as shown in the diagram above:
First we write each equation, along with its enthalpy change, on a separate line:
| Reaction 1: |
C(s) + ½O2(g) |
→ |
CO(g) |
ΔrH(reaction 1) = -110.5 kJ mol-1 |
|---|
| Reaction 2: |
CO(g) + ½O2(g) |
→ |
CO2(g) |
ΔrH(reaction 2) = -283 kJ mol-1 |
|---|
Next we draw a line under this set of equations:
| Reaction 1: |
C(s) + ½O2(g) |
→ |
CO(g) |
ΔrH(reaction 1) = -110.5 kJ mol-1 |
|---|
| Reaction 2: |
CO(g) + ½O2(g) |
→ |
CO2(g) |
ΔrH(reaction 2) = -283 kJ mol-1 |
|---|
| |
|
Now we look for substances that occur as a reactant in one equation but as a product in the other equation, for example, CO(g) is a product in reaction 1 but is a reactant in reaction 2, so these "cancel out" and we draw a line through them:
| Reaction 1: |
C(s) + ½O2(g) |
→ |
CO(g) |
ΔrH(reaction 1) = -110.5 kJ mol-1 |
|---|
| Reaction 2: |
CO(g) + ½O2(g) |
→ |
CO2(g) |
ΔrH(reaction 2) = -283 kJ mol-1 |
|---|
| |
|
Now we can add together all the substances on the "reactant" side of the equation and all the substances on the "product" side of the equation.
Note that ½O2(g) + ½O2(g) = 1O2(g) on the reactant side of the equation!
| Reaction 1: |
C(s) + ½O2(g) |
→ |
CO(g) |
ΔrH(reaction 1) = -110.5 kJ mol-1 |
|---|
| Reaction 2: |
CO(g) + ½O2(g) |
→ |
CO2(g) |
ΔrH(reaction 2) = -283 kJ mol-1 |
|---|
| |
|
| Overall reaction: |
C(s) + O2(g) |
→ |
CO2(g) |
|
|---|
And, we can add together the enthalpy change terms for each chemical reaction as well...
| Reaction 1: |
C(s) + ½O2(g) |
→ |
CO(g) |
ΔrH(reaction 1) = -110.5 kJ mol-1 |
|---|
| Reaction 2: |
CO(g) + ½O2(g) |
→ |
CO2(g) |
ΔrH(reaction 2) = -283 kJ mol-1 |
|---|
| |
|
| Overall reaction: |
C(s) + O2(g) |
→ |
CO2(g) |
ΔrH(overall) = -110.5 + -283
ΔrH(overall) = -393.5 kJ mol-1 |
|---|
↪ Back to top


