Heat of Reaction or Enthalpy of Reaction Chemistry Tutorial

Key Concepts

• Enthalpy of Reaction (Heat of Reaction) is the heat liberated or the heat absorbed when a chemical reaction takes place.

  An exothermic reaction liberates heat, temperature of the reaction mixture increases.

  An endothermic reaction absorbs heat, temperature of the reaction mixture decreases.

• The units of enthalpy of reaction, or heat of reaction, are kJ mol^-1 for a specified reactant or product.
• The enthalpy of reaction (heat of reaction) for a neutralisation reaction is known as the enthalpy of neutralisation (heat of neutralization).
• The enthalpy of reaction (heat of reaction) for a solute dissolving in a solvent is known as the enthalpy of solution (heat of solution).
• The enthalpy of reaction (heat of reaction) for a precipitation reaction is known as the enthalpy of precipitation (heat of precipitation).
• Enthalpy of reaction (heat of reaction) can be measured experimentally using a calorimeter.

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Measuring Enthalpy (heat) of Reaction Experimentally

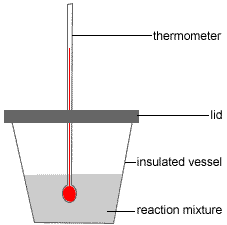
An expanded polystyrene cup (polystyrene foam or styrofoam™ cup) can be used as a calorimeter as shown in the diagram on the right because polystyrene foam is a good insulator and will prevent heat from the reaction being lost, or, heat from the surroundings entering the reaction mixture.¹

1. A known quantity of reactant is placed in a well insulated vessel (eg, a polystyrene foam cup, that is, a styrofoam™ cup)
2. The initial temperature of this reactant is recorded, T_i.
3. A known quantity of the second reactant is added, the vessel is sealed with a lid and the reaction mixture stirred.
4. The final temperature of the reaction mixture is recorded, T_f.
5. The the heat released or absorbed (the heat change) q, in joules (J), for the reaction is calculated:

   heat change = mass × specific heat capacity × temperature change

   q = m × c_g × ΔT

6. The enthalpy change, ΔH, in kJ per mole of a given reactant for the reaction is calculated:

   ΔH = heat change/1000 ÷ moles

   ΔH = q/1000 ÷ n

   Note:

   ⚛ exothermic reactions: ΔH is negative

   ⚛ endothermic reactions: ΔH is positive

Common assumptions for reaction mixtures made up of aqueous solutions:

• density of aqueous solutions assumed to be the same as for water, 1 g mL^-1 at 25°C

  example:
  100 mL of aqueous solution is said to have a mass of 100 g

• additivity of volumes of reactants in solution is assumed

  example:
  100 mL of "reactant a_(aq)" + 200 mL of "reactant b_(aq)" = 300 mL of "aqueous solution"

• specific heat capacity of the reaction mixture assumed to be the same as water,

  that is:
  specific heat capacity = 4.184 JK^-1g^-1 = 4.184 J°C^-1g^-1

• Heat is not lost to, or absorbed by, the surroundings.

Typically, the calculation for heat released or absorbed, q, for the reaction of aqueous solutions is measured in units of joules (J):

q = (mass in grams of "reactant a" + mass in grams of "reactant b") × 4.184 × (T_final - T_initial)

Enthalpy of Reaction (Heat of Reaction), ΔH, in kJ mol^-1:

ΔH = q/1000 ÷ moles of reactant

⚛ For a reaction that liberates heat, an exothermic reaction, ΔH is negative.

⚛ For a reaction that absorbs heat, an endothermic reaction, ΔH is positive.

Enthalpy of Solution (Heat of Solution) Example

In an experiment, 1.2 g of sodium hydroxide pellets, NaOH_(s), were dissolved in 100 mL of water at 25°C.

The temperature of the water rose to 27.5°C.

Calculate the enthalpy change (heat of solution) for the reaction in kJ mol^-1 of solute.

1. Calculate the heat released, q, in joules (J), by the reaction:

   q = mass(water) × specific heat capacity(water) × change in temperature(solution)
   q = m(_H2O(l)) × c_g(_H2O(l)) × (T_f - T_i)
   q = 100 × 4.184 × (27.5 - 25) = 1046 J

2. Calculate the moles of solute (NaOH_(s)):

   moles = mass ÷ molar mass
   moles (NaOH) = 1.2 ÷ (22.99 + 16.00 + 1.008)
   n(NaOH) = 0.030 mol

3. Calculate the enthalpy change, ΔH, in kJ mol^-1 of solute:

   ΔH = -q/1000 ÷ n(solute) = -1046/1000 ÷ 0.030 = -35 kJ mol^-1
   ΔH is negative because the reaction is exothermic (energy is released causing the temperature of the solution to increase).

For a more detailed tutorial go to Heat of Solution tutorial

Enthalpy of Neutralisation (Heat of Neutralization) Example

In an experiment to determine the enthalpy change, ΔH, for the neutralisation reaction:

NaOH_(aq) + HCl_(aq) → NaCl_(aq) + H₂O_(l)

The following results were obtained:

Calculate the enthalpy change, ΔH, in kJ mol^-1 of water formed for the reaction.

1. Calculate the heat released, q, in Joules (J) by the neutralisation reaction:

   q = mass(reaction mixture) × specific heat capacity(water) × change in temperature(solution)
   q = (m_a + m_b) × c_g × (T_f - T_i)
   q = (100 + 100) × 4.184 × (23.4 - 20.1)
     = 200 × 4.184 × 3.3
     = 2761.44 J

2. Calculate the moles of reactants:

   moles = molarity × volume

   moles (NaOH) = 0.50 mol L^-1 × (100 × 10^-3) L = 0.05 mol
   moles (HCl) = 0.50 mol L^-1 × (100 × 10^-3) L = 0.05 mol

   NaOH_(aq) and HCl_(aq) are in 1:1 mole ratio which is an exact stoichiometric ratio as shown by the neutralisation equation.
   0.05 mole of NaOH(aq) reacts with 0.05 mole HCl(aq) to produce 0.05 mole of water.

3. Calculate the enthalpy (heat) of reaction, ΔH, in kJ mol^-1

   Since the reactants are present in a 1:1 stoichiometric ratio, 0.05 mole of NaOH(aq) reacts with 0.05 mole HCl(aq) to produce 0.05 mole of water,
   moles (H₂O_(l)) = n(H₂O_(l)) = 0.05 mol

   ΔH = -q/1000 ÷ n(H₂O_(l))
       = -2761.44/1000 ÷ 0.05
       = -55.2 kJ mol^-1
   ΔH is negative because the reaction is exothermic.

For a more detailed tutorial go to Heat of Neutralisation tutorial

Enthalpy of Precipitation (Heat of Precipitation) Example

50 mL of 0.20 mol L^-1 lead(II) nitrate solution, Pb(NO₃)_2(aq), at 19.6°C was added to 30 mL of a solution containing excess potassium iodide, KI_(aq) also at 19.6°C.

The solutions reacted to form a yellow lead(II) iodide precipitate, PbI_2(s), and the temperature of the reaction mixture increased to 22.2°C.

Pb(NO₃)_2(aq) + 2KI_(aq) → PbI_2(s) + 2KNO_3(aq)

Calculate the enthalpy change per mole of lead(II) iodide precipitated for the reaction.

1. Calculate the heat released, q, in Joules (J), by the precipitation reaction:

   q = mass × specific heat capacity × change in temperature
   q = [m_Pb(NO3)2(aq) + m_KI(aq)] × c_g × (T_f - T_i)
   q = [50 + 30] × 4.184 × (22.2 - 19.6)
     = 870.27 J

2. Calculate the moles of species specified, n(PbI_2(s)):

   From the equation, 1 mole Pb(NO₃)_2(aq) reacts with excess KI_(aq) to produce 1 mol PbI_2(s)
   moles Pb(NO₃)_2(aq) = moles PbI_2(s)

   n(Pb(NO₃)_2(aq)) = n(PbI_2(s))

   n(Pb(NO₃)_2(aq)) = molarity × volume
   n = moles(Pb(NO₃)_2(aq))
     = moles(PbI_2(s))
     = 0.20 × 50 × 10^-3
     = 0.010 mol

3. Calculate the enthalpy of precipitation (heat of precipitation), ΔH, in kJ mol^-1 of PbI_2(s):

   ΔH = -q/1000 ÷ n
   ΔH = -0.870/1000 ÷ 0.010
       = -87 kJ mol^-1
   ΔH is negative because the reaction is exothermic (energy was released causing the temperature to increase).

Footnotes