Molar Enthalpy of Combustion (Molar Heat of Combustion) of Fuels Chemistry Tutorial

Key Concepts

⚛ Heat of combustion is also known as enthalpy of combustion, Δ_cH

⚛ When a substance undergoes combustion it releases energy.

Combustion is always exothermic, the enthalpy change for the reaction is negative, Δ_cH has a negative sign.

⚛ Molar Heat of Combustion (molar enthalpy of combustion) of a substance, Δ_cH_m, is the heat liberated when 1 mole of the substance undergoes complete combustion with oxygen at constant pressure.

⚛ By convention, the molar heat of combustion (molar enthalpy of combustion) is given in tables as a positive value.

⚛ Tabulated values of molar enthalpy of combustion can be used to determine the amount of heat energy released (q) when a known amount of the substance (n) undergoes complete combustion:

q = n × molar enthalpy of combustion

⚛ Molar Heat of Combustion (molar enthalpy of combustion) of a pure substance can be determined experimentally: energy from the combustion of a known amount of fuel is used to heat a known mass of water and the increase in water temperature is recorded.

Step 1: Calculate moles of fuel consumed in combustion reaction

n(fuel) = m(fuel) ÷ M_r(fuel)

Step 2: Calculate the amount of energy absorbed by the water

q(water) = m(water) × c_g × ΔT

Step 3: Calculate the amount of energy released by the combustion of the fuel assuming no heat loss

q(fuel) = −q(water)

Step 4: Calculate energy released per mole of fuel combusted

Δ_cH_m(fuel) = q(fuel) ÷ n(fuel)

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Using Tabulated Values of Molar Enthalpy of Combustion in Calculations

Hydrocarbons, such as alkanes, and alcohols, such as alkanols, can be used as fuels.

When an alkane undergoes complete combustion in excess oxygen gas the products of the reaction are carbon dioxide (CO_2(g)) and water (H₂O_(g)) which will condense to H₂O_(l) at room temperature and pressure).

alkane + excess oxygen gas → carbon dioxide gas + water vapor

The molar heat of combustion of the alkane (molar enthalpy of combustion of the alkane) is the amount of heat energy released when 1 mole of the alkane combusts in excess oxygen gas.

When an alkanol undergoes complete combustion in excess oxygen gas the products of the reaction are carbon dioxide (CO_2(g)) and water (H₂O_(g) which will condense to H₂O_(l) at room temperature and pressure).

alkanol + excess oxygen gas → carbon dioxide gas + water vapor

The molar heat of combustion of the alkanol (molar enthalpy of combustion of the alkanol) is the amount of heat energy released when 1 mole of the alkanol combusts in excess oxygen gas.

In order to determine the molar heat of combustion, we need to be able to determine how many moles of the substance were consumed in the combustion reaction so the substance must be a pure substance.⁽¹⁾

The molar heat of combustion (molar enthalpy of combustion) of some common alkanes and alcohols used as fuels is tabulated below in units of kilojoules per mole (kJ mol^-1)⁽²⁾.

Note that the chemical equations representing each of the combustion reactions is balanced so that 1 mole of the substance combusted, the fuel, is used.
The combustion reaction occurs in excess oxygen gas, excess O_2(g), so it is quite OK to use fractions of O_2(g) to balance the equation because we are really only interested in the energy released per mole of the fuel, not per mole of oxygen gas.

Pure Substance (fuel)	Tabulated Values of Molar Heat of Combustion (kJ mol^-1)	Combustion Reaction	Δ_cH_m (kJ mol^-1)
methane	890	CH_4(g) + 2O_2(g) → CO_2(g) + 2H₂O_(l)	−890
ethane	1560	C₂H_6(g) + ⁷/₂O_2(g) → 2CO_2(g) + 3H₂O_(l)	−1560
propane	2220	C₃H_8(g) + 5O_2(g) → 3CO_2(g) + 4H₂O_(l)	−2220
butane	2874	C₄H_10(g) + ¹³/₂O_2(g) → 4CO_2(g) + 5H₂O_(l)	−2874
octane	5460	C₈H_18(g) + ²⁵/₂O_2(g) → 8CO_2(g) + 9H₂O_(l)	−5460
methanol (methyl alcohol)	726	CH₃OH_(l) + ³/₂O_2(g) → CO_2(g) + 2H₂O_(l)	−726
ethanol (ethyl alcohol)	1368	C₂H₅OH_(l) + 3O_2(g) → 2CO_2(g) + 3H₂O_(l)	−1368
propan-1-ol (1-propanol)	2021	C₃H₇OH_(l) + ⁹/₂O_2(g) → 3CO_2(g) + 4H₂O_(l)	−2021
butan-1-ol	2671	C₄H₉OH_(l) + 6O_2(g) → 4CO_2(g) + 5H₂O_(l)	−2671

From the table we see that 1 mole of methane gas, CH_4(g), undergoes complete combustion in excess oxygen gas releasing 890 kJ of heat.
The molar heat of combustion of methane gas is tabulated as a positive value, 890 kJ mol^-1.
The enthalpy change for the combustion of 1 mole of methane gas is given in the table as a negative value, Δ_cH_m = −890 kJ mol^-1, because the reaction produces energy (it is an exothermic reaction).
We could write a chemical equation to represent the combustion of 1 mole of methane gas as:

CH_4(g) + 2O_2(g) → CO_2(g) + 2H₂O_(g) Δ_cH_m = −890 kJ mol^-1

But how much energy is released if 2 moles of methane undergoes complete combustion?
When we write a chemical equation for this reaction we must multiply every term by two ( × 2) including the value of Δ_cH_m:

2 × CH_4(g) + 2 × 2O_2(g) → 2 × CO_2(g) + 2 × 2H₂O_(g) Δ_cH = 2 × −890 kJ mol^-1

2CH_4(g) + 4O_2(g) → 2CO_2(g) + 4H₂O_(g) Δ_cH = −1780 kJ mol^-1

2 moles of methane would combust completely to release 2 × 890 = 1780 kJ of heat.

Similarly, if we have only half a mole of methane gas that undergoes complete combustion we must multiply every term in the chemical equation, including the value of Δ_cH_m, by ½ as shown in the chemical equations below:

½ × CH_4(g) + ½ × 2O_2(g) → ½ × CO_2(g) + ½ × 2H₂O_(g) Δ_cH = ½ × −890 kJ mol^-1

½CH_4(g) + O_2(g) → ½CO_2(g) + H₂O_(g) Δ_cH = −445 kJ mol^-1

½ mole of methane would combust to release ½ × 890 = 445 kJ of heat.

In general, the amount of heat energy released by the combustion of n moles of fuel is equal to the value of the molar heat of combustion of the fuel multiplied by the moles of fuel combusted

heat released (kJ) = n (mol) × molar enthalpy of combustion (kJ mol^-1)

(See the Enthlapy Change Calculations for a Chemical Reaction Tutorial for more examples of these types of calculations)

In this section we looked at how to use tables of values for the molar enthalpy of combustion of pure substances to calculate how much heat energy would be released when known amounts of the substance were combusted in excess oxygen gas.
But where do these values come from?
Molar enthalpy of combustion values can be determined using laboratory experiments.
In the next section we will discuss an experiment you could do to determine the molar heat of combustion of an alcohol.

↪ Back to top

Experiment to Measure Molar Heat of Combustion of a Liquid Fuel in the Lab

In the school laboratory it is possible to determine the molar heat of combustion (enthalpy of combustion) of a liquid fuel such as an alcohol using the procedure outlined below:⁽³⁾

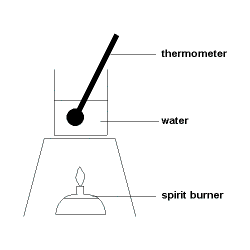
Step 1: A known quantity of water is placed in a flask, beaker or can.

Step 2: A thermometer is positioned with its bulb (reservoir) near the middle of the volume of water.

Step 3: A known quantity of fuel, such as an alcohol (alkanol), is placed in the spirit burner.

Step 4: The initial temperature of the water is measured and recorded (T_i).

Step 5: The wick on the spirit burner is lit, burning the fuel, and heating the water.

Step 6: When the temperature of the water has risen an appreciable amount, the spirit burner is extinguished and the maximum temperature reached is recorded as the final temperature (T_f).

Step 7: The final quantity of fuel is measured and recorded.

Typical results for an experiment where the energy released by the complete combustion of ethanol is used to heat 200 g of water are shown below:

initial water temperature (T_i) = 20.0°C	intial mass burner + ethanol = m_i = 37.25 g
final water temperature (T_f)= 75.0°C	final mass burner + ethanol = m_f = 35.50 g

change in water temperature ΔT = T_f − T_i = 75.0 − 20.0 = 55.0°C	mass ethanol used in combustion reaction m(ethanol) = m_i − m_f = 37.25 − 35.50 = 1.75 g

Note:

Temperature of the water increases because combustion of the fuel releases energy which heats the water.
Mass of the fuel decreases because it is being consumed in the combustion reaction.

The results of the experiment can be used to calculate the molar enthalpy of combustion of the fuel:

Step 1. Calculate moles (n) of fuel used in the combustion reaction :

n(fuel) = m(fuel) ÷ M(fuel)

Step 2. Calculate energy absorbed by the water to increase its temperature:

q = m(water) × c_g(water) × ΔT(water)

Step 3. Calculate energy released by the combustion reaction:

Assume all the heat produced from burning the fuel has gone into heating the water, that is, no heat has been wasted.

energy released by combustion reaction = −energy absorbed by water = −q

Step 4. Calculate the molar heat of combustion of fuel (molar enthalpy of combustion of fuel)

Δ_cH_m(fuel) = −q ÷ n(fuel)

Using the experimental results tabulated above, we can use these steps to calculate the molar enthalpy of combustion of ethanol::

Step 1: Calculate moles (n) of fuel used used in the combustion reaction

moles = mass ÷ molar mass

mass ethanol used = m(C₂H₅OH) = 1.75 g (from experiment)

molar mass (M) of ethanol (C₂H₅OH)

M(C₂H₅OH) = (2 × 12.01) + (6 × 1.008) + 16.00 (atomic weights from periodic table)

M(C₂H₅OH) = 46.1 g mol^-1

n(C₂H₅OH)) = m(C₂H₅OH) ÷ M(C₂H₅OH)

= 1.75 g ÷ 46.1 g mol^-1

= 0.0380 mol

Step 2: Calculate energy absorbed by the water to increase its temperature:

energy absorbed by water = specific heat capacity of water × mass of water × change in water temperature

specific heat capacity of water = c_g = 4.184 J °C^-1 g^-1 (from a data sheet)

mass water = 200 g (from the experiment)

change in water temperature = 55.0°C (from the experiment)

energy absorbed by water = 4.184 J ~~°C^-1 g^-1~~ × 200 g × 55.0°C = 46024 J

Convert energy in J to kJ by dividing by 1000:

energy = 46024 J ÷ 1000 J/kJ = 46.024 kJ

Note: we can only justify the use of 3 significant figures, so:
energy absorbed by water = 46.0 kJ

Step 3. Calculate energy released by the combustion reaction:

Assume all the heat produced from burning the ethanol has gone into heating the water, that is, no heat has been wasted.

energy released by combustion reaction = −energy absorbed by water = −q = −46.0 kJ

Step 4: Calculate the molar heat of combustion of ethanol (molar enthalpy of combustion of ethanol):

Δ_cH_m(fuel) = −q ÷ n(fuel)

heat released = −q = −46.0 kJ

amount of ethanol combusted = n(CH₃CH₂OH_(l)) = 0.0380 mol

Δ_cH_m(CH₃CH₂OH_(l)) = −46.0 kJ ÷ 0.0380 mol = −1210 kJ mol^-1

Note: 3 significant figures are justified.

Therefore the molar heat of combustion of ethanol is 1210 kJ mol^-1
(The molar enthalpy of combustion of ethanol is 1210 kJ mol^-1).

Note: the enthalpy change for the reaction is negative because the reaction is exothermic, so the enthalpy change for the reaction is −1210 kJ mol^-1,
Δ_cH_m(CH₃CH₂OH_(l)) = −1210 kJ mol^-1

The experimentally determined value for the molar heat of combustion of ethanol is usually less than the accepted tabulated value of 1368 kJ mol^-1 because :

(i) some heat is always lost to the atmosphere

(ii) some heat is always lost by heating the vessel.

The design of the experiment can be improved by trying to minimise the heat lost to the surroundings, for example, by surrounding the whole experimental set-up with metal walls.
By far the best way of minimising heat loss to the surroundings is to use a bomb calorimeter.

↪ Back to top

Worked Example: Calculating Molar Enthalpy of Combustion Using Experimental Results

The Problem: A spirit burner used 1.00 g of methanol, CH₃OH_(l), to raise the temperature of 100.0 g of water in a metal can from 25.0 °C to 55.0 °C.

Assuming the heat capacity of water is 4.184 J °C^-1 g^-1, calculate the molar enthalpy of combustion of methanol in kJ mol^-1.

Solving the Problem using the StoPGoPS model for problem solving:

STOP!	State the question.	What is the question asking you to do? Determine (calculate) the molar enthalpy of combustion of methanol in kJ mol^-1 Δ_cH_m(CH₃OH_(l)) = ? kJ mol^-1
PAUSE!	Pause to Plan.	What information (data) have you been given? Extract the data from the question: m(CH₃OH) = mass methanol used = 1.00 g m(H₂O) = mass water heated = 100.0 g c_g = heat capacity of water = 4.184 J °C^-1 g^-1 T_i = temperature of water before methanol combustion = 25.0 °C T_f = temperature of water after methanol combustion = 55.0 °C What is your plan for solving this problem? Step 1: Calculate the moles of methanol, n(CH₃OH), combusted: n(CH₃OH) = m(CH₃OH) ÷ M(CH₃OH) Step 2: Calculate the energy absorbed by the water, q(absorbed): q(absorbed by water) = m(H₂O) × c_g(H₂O) × (T_f − T_i) Step 3: Calculate the amount of heat released by combustion of methanol Assume no heat lost, all the energy released by combustion of methanol, q(released), is used to heat the water, q(absorbed): q(released) = −q(absorbed) Step 4: Calculate molar enthalpy of combustion of methanol: Δ_cH_m(CH₃OH_(l)) = q(released) ÷ n(CH₃OH) = ? J mol^-1 Divide molar heat of combustion of methanol in J mol^-1 by 1000 J/kJ to get molar heat of combustion in kJ mol^-1
GO!	Go with the Plan.	Step 1: Calculate the moles of methanol, n(CH₃OH), combusted: n(CH₃OH) = m(CH₃OH) ÷ M(CH₃OH) M_r(CH₃OH) = molar mass(CH₃OH) M_r(CH₃OH) = 12.01 + (4 × 1.008) + 16.00 = 32.042 g mol^-1 n(CH₃OH) = 1.00 g ÷ 32.042 g mol^-1 = 0.03121 mol Step 2: Calculate the energy absorbed by the water, q(absorbed): q(absorbed by water) = m(H₂O) × c_g(H₂O) × (T_f − T_i) q(absorbed by water) = 100.0 g × 4.184 J ~~g^-1 °C^-1~~ × (55.0 − 25.0) °C = 100.0 × 4.184 × 30.0 = 12552 J Step 3: Calculate the amount of heat released by combustion of methanol Assume no heat lost, all the energy released by combustion of methanol, q(released), is used to heat the water, q(absorbed): q(released) = −q(absorbed) = −12552 J Step 4: Calculate molar enthalpy of combustion of methanol: Δ_cH_m(CH₃OH_(l)) = q(released) ÷ n(CH₃OH) = −12552 J ÷ 0.03121 mol = −402179 J mol^-1 Divide molar heat of combustion of methanol in J mol^-1 by 1000 J/kJ to get molar heat of combustion in kJ mol^-1 Δ_cH_m(CH₃OH_(l)) = −402179 J mol^-1 ÷ 1000 J/kJ = −402 kJ mol^-1 (Only 3 significant figures are justufied)
PAUSE!	Ponder Plausability.	Have you answered the question that was asked? Yes, we have calculated the the molar enthalpy of combustion of methanol in kJ mol^-1 Is your solution to the question reasonable? Let's work backwards: use our calculated value of molar enthalpy of combustion to calculate the temperature increased for 100 g of water when 1 g of methanol combusts. heat of combustion ≈ 400 kJ mol^-1 n(CH₃OH) ≈ 1.00 g ÷ 32 ≈ 0.03 mol heat released ≈ 400 kJ mol^-1 × 0.03 mol = 12 kJ = 12,000 J heat absorbed by water ≈ 12,000 J = m(water) × c_g × ΔT 12,000 ≈ 100 × 4 × ΔT ΔT = 30 °C Since this value for the temperature change expected is the same as that given in the question (55 °C − 25 °C = 30 °C) we are reasonably confident that our answer for the heat of combustion is plausible.
STOP!	State the solution.	What is the molar enthalpy of combustion of methanol in kJ mol^-1 ? Δ_cH_m(CH₃OH_(l)) = −402 kJ mol^-1

↪ Back to top

Sample Question

A portable can of fuel for welding contains 150.0 g of a mixture of two gases under pressure: 35%(m/m) propane and 65%(m/m) butane.

The molar enthalpies of combustion of propane and butane are tabulated as 2220 kJ mol^-1 and 2874 kJ mol^-1 respetively.

Calculate the maximum energy output in kilojoules for the 150.0 g of fuel in the can.

↪ Back to top

Footnotes:

(1) If the substance to be combusted is not a pure substance, you can still determine how much energy is released when it combusts, BUT, the units will not be kilojoules per mole.
If you know the mass of mixture combusted you could determine the energy released in units of kilojoules per gram for instance, or kilojoules per kilogram, etc.
If you know the volume of a liquid fuel, you could determine the energy released in units of kilojoules per milliltre or kilojoules per litre etc.
For example, biodiesel and vegetable oils are both mixtures of substances so their heats of combustion are usually given in units of J g^-1

(2) The Ninth International Conference on Weights and Measures (1948) recommended the use of the joule (volt coulomb) as the unit of heat.
The joule is a derived SI unit for the measurement of energy.
The SI base unit for the measurement of energy is kg m² s^-2
1 J = 1 kg m² s^-2

The calorie is also a unit of heat, 1 cal = 4.1840 J
If you need to convert between joules (J) and calories (cal) go to Energy Conversions Tutorial

(3) An alternative method for determining heat of combustion (enthalpy of combustion) using a bomb calorimeter is outlined in the calorimetry tutorial.

↪ Back to top