AUS-e-TUTE logo

Degree of Unsaturation Calculations Tutorial

Key Concepts

Assumed Knowledge

Quicklinks to Sections on This Page

  1. Degree of Unsaturation: Hydrocarbons
  2. Degree of Unsaturation: Halogenated Hydrocarbons
  3. Degree of Unsaturation: Oxidized Hydrocarbons
  4. Degree of Unsaturation: Nitrogenated Organic Compounds
  5. Degree of Unsaturation Calculator
  6. Worked Examples
  7. Problem Solving
  8. Resources for Teachers and Students

Degree of Unsaturation: Hydrocarbons

A hydrocarbon is a molecule containing only carbon and hydrogen atoms.

An acyclic hydrocarbon is a straight chain hydrocarbon. There are no rings in an acyclic hydrocarbon.

A saturated acyclic hydrocarbon is a molecule containing only single bonds between the carbon atoms (C-C).(1) The general formula of a saturated hydrocarbon is CnH2n+2

An unsaturated acyclic hydrocarbon is a molecule containing at least one double bond or triple bond between carbon atoms. Each time a double bond is formed between two carbon atoms (C=C), 2 hydrogen atoms are lost from the molecule, the molecule becomes deficient in hydrogen. Each time a triple bond is formed between two carbon atoms (C≡C), 4 hydrogen atoms are lost from the molecule, the molecule is more deficient in hydrogen.

The "degree of unsaturation" indicates:

A saturated acyclic hydrocarbon has no double nor triple bonds, its degree of unsaturation is 0. It is not deficient in hydrogen so its index of hydrogen deficiency is likewise 0. It contains no double bonds so its double bond equivalents is also 0

Butane is a saturated acyclic hydrocarbon containing 4 carbon atoms (n=4).
The maximum number of hydrogen atoms that can be present for a 4 carbon chain is = 2n + 2 = 2×4 + 2 = 10
The molecular formula for butane is C4H10, there are 10 hydrogen atoms present.
The number of hydrogen atoms present = the maximum number of hydrogen atoms possible, therefore butane is saturated in hydrogen.
A structural formula for butane is given below:

  H
|		   H
|		   H
|		   H
|		   degree of unsaturation = 0
index of hydrogen deficiency = 0
double bond equivalents = 0
H- C - C - C - C -H
  |
H		   |
H		   |
H		   |
H		  

Now let us consider but-1-ene which we could imagine being formed by the removal of 1 hydrogen from the first carbon atom in the chain and the removal of 1 hydrogen atom from the second carbon atom in the chain resulting in the formation of a double bond between the first and second carbon atoms as shown below:

  H
|		   H
|		   H
|		   H
|		  
H- C = C - C - C -H
          |
H		   |
H		  

But-1-ene, C4H8, is an unsaturated acyclic hydrocarbon because it contains a double bond between carbon atoms in the straight chain.
Its double bond equivalents is 1 because it contains 1 double bond.
It is deficient in 2 hydrogens, but we divide by 2 to arrive at its index of hydrogen deficiency, that is,
index of hydrogen deficiency = 2 ÷ 2 = 1
We calculate the degree of unsaturation by subtracting the number of hydrogens present (8) from the maximum number of hydrogens the chain could possibly have (2n+2) and then dividing by 2:
degree of unsaturation = (2×4 + 2 - 8) ÷ 2 = 2 ÷ 2 = 1

Unfortunately there is more than one way to arrange 4 carbon atoms and 8 hydrogen atoms, in other words, there are structural isomers of but-1-ene.
Consider cyclobutane shown below:

  H
|		   H
|		  
H- C - C -H
  |   |  
H- C - C -H
  |
H		   |
H		  

Although this is a saturated cyclic hydrocarbon(2), 2 H atoms have been removed on order to produce a ring, hence it is deficient in 2 hydrogens so its index of hydrogen deficiency is 2/2 = 1.
Cyclobutene has the molecular formula C4H8
Degree of unsaturation = (maximum no. H atoms possible - no. H atoms present) ÷ 2
degreee of unsaturation = ((2×4 + 2) - 8)/2 = 1
Hence its double bond equivalents = 1, this means that the act of turning a straight chain into a cyclic molecule is equivalent to the formation of a double bond for the purposes of this calculation (but certainly not equivalent in terms of the molecule's reactivity!).

Now consider a 4 carbon hydrocarbon chain that contains 2 double bonds, C4H6:

  H
|		   H
|		   H
|		   H
|		  
H- C = C - C = C -H

Degree of unsaturation = (maximum no. H atoms possible - no. H atoms present) ÷ 2
Degree of unsaturation = (2×n + 2 - H atoms present)/2
Degree of unsaturation = (2×4 + 2 - 6)/2 = 4/2 = 2
This molecule has 2 double bonds, so its degree of unsaturation is 2.

However, other structural isomers are possible for C4H6, for example:

          H
|		   H
|		  
H- C ≡ C - C - C -H
          |
H		   |
H		  

Degree of unsaturation = (maximum no. H atoms possible - no. H atoms present) ÷ 2
Degree of unsaturation = (2×n + 2 - H atoms present)/2
Degree of unsaturation = (2×4 + 2 - 6)/2 = 4/2 = 2
This molecule has no double bonds, but it does have a triple bond. 1 triple bond is equivalent to 2 double bonds for the purposes of this calculation.
The formation of 2 double bonds requires the loss of 4 hydrogen atoms, similarly, the formation of 1 triple bond requires the loss of 4 hydrogen atoms.

Ofcourse there is also the possibility of a cyclic compound with the molecular formula C4H6 also:

H- C = C -H
  |   |  
H- C - C -H
  |
H		   |
H		  

Degree of unsaturation = (maximum no. H atoms possible - no. H atoms present) ÷ 2
Degree of unsaturation = (2×n + 2 - H atoms present)/2
Degree of unsaturation = (2×4 + 2 - 6)/2 = 4/2 = 2
This molecule has 1 double bond and is cyclic. 1 ring + 1 double bond is equivalent to 2 double bonds, or to 1 triple bond, for the purposes of this calculation.
The formation of 1 ring and 1 double bond requires the loss of 4 hydrogen atoms, similarly the formation of 1 triple bond requires the loss of 4 hydrogen atoms, likewise the formation of 2 double bonds requires the loss of 4 hydrogen atoms.

Degree of Unsaturation Calculations
for Hydrocarbons

For the molecular formula CnHm :

degree of unsaturation = (2×n +2 -m) ÷ 2

Possible structural features for
different degrees of unsaturation
  Number of
Degree of
unsaturation 		C=C C≡C rings
0 0 0 0
1 1 0 0
0 0 1
2 2 0 0
0 1 0
1 0 1

Back to the top

Degree of Unsaturation: Halogenated Hydrocarbons

Consider the structure of a molecule of the saturated hydrocarbon butane (C4H10) in which 2 of the hydrogen atoms have been replaced by halogen atoms, bromine for example (C4H8Br2):

  H
|		   H
|		   H
|		   H
|		  
Br- C - C - C - C -Br
  |
H		   |
H		   |
H		   |
H		  

There are no double bonds, no triple bonds, no rings, so we would conclude that this is still a saturated compound, even though it appears to be deficient in hydrogen atoms. For the purpose of calculating a degree of unsaturation, each halogen atom is treated as if it were a hydrogen atom.

Let X represent any halogen (Group 17) element:
Degree of unsaturation = [maximum no. H atoms possible -(no. H atoms present + no. X atoms present)] ÷ 2
Degree of unsaturation = (maximum no. H atoms possible -no. H atoms present - no. X atoms present) ÷ 2

Degree of Unsaturation Calculations
for Halogenated Hydrocarbons

For halogenated hydrocarbon CnHmXk
(X is fluorine, chlorine, bromine or iodine):

degree of unsaturation = (2×n +2 -m -k) ÷ 2

For C4H8Br2, n=4, m=8, k=2 and

degree of unsaturation = (2×n +2 -m -k) ÷ 2 = (2×4 +2 -8 -2)/2 = 0/2 = 0

Degree of unsaturation is 0, so there are no double bonds, no triple bonds, no rings.

Now consider C4H6Br2.
n=4, m=6, k=2 and

degree of unsaturation = (2×n +2 -m -k) ÷ 2 = (2×4 +2 -6 -2)/2 = 2/2 = 1

Since the degree of saturation is 1, we expect the structure to contain either a double bond or a ring. Possible structures are:

  H
|		   H
|		   H
|		   H
|		  
Br- C = C - C - C -Br
          |
H		   |
H		  
or
  H
|		   H
|		  
H- C - C -H
  |   |  
Br- C - C -Br
  |
H		   |
H		  

and other structural isomers of each of these is also possible.

If the molecular formula were C4H4Br2, then
n=4, m=4, k=2
degree of unsaturation = (2×n +2 -m -k)/2 = (2×4 +2 -4 -2)/2 = 4/2 = 2

When the degree of unsaturation is 2, possible structures include:

Back to the top

Degree of Unsaturation: Oxidized Hydrocarbons

An oxidized hydrocarbon is a molecule that contains carbon, hydrogen and oxygen.

Consider butan-1-ol, a saturated acyclic alcohol:

  H
|		   H
|		   H
|		   H
|		  
H- C - C - C - C -OH
  |
H		   |
H		   |
H		   |
H		  

There are no double bonds present, no triple bonds, and it is not cyclic, therefore we predict the degree of unsaturation to be 0.

The maximum number of hydrogens that could be present in a 4 carbon chain is 2n+2 = 2× 4 + 2 = 10
The number of hydrogen atoms present in butan-1-ol is 10
This molecule is fully saturated in hydrogen atoms, there is no hydrogen deficiency, so its index of hydrogen deficiency is 0
Hence its degree of unsaturation is also 0, and its double bond equivalents is likewise 0
Butan-1-ol is a saturated molecule.

Compare this to a molecule of butanal(3), C4H8O, also an oxidised form of butane:

  H
|		   H
|		   H
|		   H
|		  
H- C - C - C - C =O
  |
H		   |
H		   |
H		      

The introduction of a carbonyl group (C=O) reduces the number of hydrogen atoms in the molecule by 2 compared to the saturated butane molecule. There is a hydrogen deficiency of 2, its index of hydrogen deficiency is 2/2 = 1
Degree of unsaturation = (maximum number of hydrogen atoms possible - number of hydrogen atoms present)/2
degree of unsaturation = (2n +2 - number of hydrogen atoms present)/2
degree of unsaturation = (2×4 +2 - 8)/2 = 2/2 = 1
Since there is 1 degree of unsaturation the structure must contain either a double bond or a ring, which indicates that the double bond between the C and O atoms is equivalent to a double bond between two adjacent carbon atoms for the purposes of this calculation.

This makes more sense when we consider the following structural isomer of C4H8O as shown below:

  H
|		   H
|		   H
|		   H
|		  
H- C = C - C - C -OH
          |
H		   |
H		  

This structural isomer is clearly an unsaturated alcohol with one carbon-carbon double bond. The degree of unsaturation is 1.

Another structural isomer of C4H8O is shown below:

  H
|		   H
|		  
H- C - C -OH
  |   |  
H- C - C -H
  |
H		   |
H		  

This molecule has 1 degree of unsaturation which has resulted from the formation of a cyclic structure.

Next, let us consider an oxidised hydrocarbon with the formula C4H8O2
degree of unsaturation = (maximum no. H atoms possible - no. H atoms present)/2
degree of unsaturation = (2×n +2 - no. H atoms present)/2
degree of unsaturation = (2×4 +2 - 8)/2 = 2/2 = 1
Which indicates a 4 carbon chain containing one C=C as shown below:

  H
|		   H
|		   H
|		   H
|		  
H- C = C - C - C -OH
          |
H		   |
OH		  

Or, it might be cyclic structure with no double bonds as shown below:

  H
|		   H
|		  
H- C - C -OH
  |   |  
H- C - C -OH
  |
H		   |
H		  

Or, it might be a straight chain of 4 carbon atoms with only single bonds between the carbon atoms, but with one carbonyl group as shown below(4):

  H
|		   H
|		   H
|		   O
|| 		 
H- C - C - C - C -OH
  |
H		   |
H		   |
H		      

The structural isomer above is a saturated carboxylic acid with 1 degree of unsaturation.

Other structural isomers are also possible:

  H
|		   H
|		   O
||		   H
|		  
H- C - C -O- C - C -H
  |
H		   |
H		       |
H		  

This structural isomer is an ester with 1 degree of unsaturation due solely to the presence of the C=O group.

How do we calculate the degree of unsaturation of oxidised hydrocarbons? Exactly the same way as we do for hydrocarbons, we just ignore the presence of oxygen atoms in the calculation.

Degree of Unsaturation Calculations
for Oxidised Hydrocarbons

For the molecular formula CnHmOl :

degree of unsaturation = (2×n +2 -m) ÷ 2

However, we need to interpret the results of the calculation with great caution.

CnHmOl with 1 degree of unsaturation could be any of the following:

As the number of degrees of unsaturation increase, the number of possible structural isomers will likewise increase.
All we can say with any degree of certainty is that at least one of the possible structural isomers will contain the same number of C=C as the calculated degree of unsaturation.

Back to the top

Degree of Unsaturation: Nitrogenated Organic Compounds

Consider butane, C4H10, as an example of a saturated acyclic hydrocarbon.

  H
|		   H
|		   H
|		   H
|		   degree of unsaturation = 0
index of hydrogen deficiency = 0
double bond equivalents = 0
H- C - C - C - C -H
  |
H		   |
H		   |
H		   |
H		  

Butan-1-amine, C4H11N, is also a saturated organic compound:

  H
|		   H
|		   H
|		   H
|		   H
|		  
H- C - C - C - C - N -H
  |
H		   |
H		   |
H		   |
H		      

Butan-1-amine, C4H11N, has 1 more hydrogen atom than butane, C4H10.
Every time 1 nitrogen atom is added to an organic compound, 1 more hydrogen is added to the total of hydrogen atoms present in the saturated acyclic compound.
If 2 nitrogen atoms were added to the molecule, then 2 hydrogen atoms would be added to make the molecule saturated.

Hence we can say that for a compound with the molecular formula CnHmNj:

degree of unsaturation = 2×n + 2 - m + j
2

For C4H11N
n = 4
m = 11
j = 1

degree of unsaturation = 2×n + 2 - m + j
2
  = 2×4 + 2 - 11 + 1
2
  = 10 - 11 + 1
2
  = 0

Therefore, C4H11N is a saturated molecule. It contains no double nor triple bonds and it cannot contain a ring.

A molecule of butanenitrile, C4H7N, is shown below:

    H
|		   H
|		   H
|		        
H - C - C - C - C ≡ N
    |
H		   |
H		   |
H		        

This molecular contains a triple bond (C≡N), hence its degree of unsaturation is 2.

Or, we can calculate its degree of unsaturation using its molecular formula C4H7N as shown below:
n = 4
m = 7
j = 1

degree of unsaturation = 2×n + 2 - m + j
2
  = 2×4 + 2 - 7 + 1
2
  = 10 - 7 + 1
2
  = 4
2
  = 2

What if the organic compound contains both oxygen and nitrogen? How would we calculate the degree of unsaturation?

Consider the primary alkanamide butanamide, C4H9NO, whose structural formula is given below:

  H
|		   H
|		   H
|		   O
||		      
H- C - C - C - C - N -H
  |
H		   |
H		   |
H		       |
H		  

This molecule contains one double bond (C=O) so we conclude that its degree of unsaturation is 1.

To calculate its degree of unsaturation we ignore the number of oxygen atoms (see the section above) and use the same equation as above:
n = 4
m = 9
j = 1

degree of unsaturation = 2×n + 2 - m + j
2
  = 2×4 + 2 - 9 + 1
2
  = 10 - 9 + 1
2
  = 2
2
  = 1

The calculation agrees with our inspection of the structural formula, butanamide has 1 degree of unsaturation.

To summarise:

Degree of Unsaturation Calculations
for organic compounds

For the molecular formula CnHmNjOl :

degree of unsaturation = (2×n +2 -m +j) ÷ 2

Back to the top

Degree of Unsaturation Calculator

Uses this calculator to calculate the degree of unsaturation of an organic compound containing carbon and hydrogen and/or oxygen and/or nitrogen and/or halogen atoms (such as fluorine, chlorine, bromine or iodine).

Step 1: Enter the number of carbon (C), hydrogen (H), nitrogen (N), oxygen (O) or halogen (X) atoms into the boxes below.

If there are no oxygen atoms, do not type a number in the box to the right of the "O", leave this box blank.
Similarly if there are no halogen atoms, do not type a number in the box to the right of the "X", leave this box blank.
If there is 1 oxygen atom, type the number 1 in the box to the right of the "O".
If there is 1 nitrogen atom, type the number 1 in the box to the right of the "N".
If there is 1 halogen atom, type the number 1 in the box to the right of the "X".
For example, if the molecular formula is C2H6O
Type a 2 into the box to the right of the C
Type a 6 into the box to the right of the H
Leave the box to the right of the N empty
Type a 1 into the box to the right of the O
Leave the box to the right of the X empty

Step 2: Click the calculate button. The degree of unsaturation will be displayed under the buttons.

Step 3: Click the "Clear" button to clear the boxes and start a new calculation.

Degree of Unsaturation Calculator

CHNOX

Back to the top

Worked Examples: Degree of Unsaturation

Question 1:

Determine the degree of unsaturation of the molecule shown below:

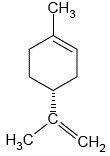
limonene

Answer 1:

1 ring = 1 degree of unsaturation

2 double bonds = 2 degrees of unsaturation

degree of unsaturation in molecule = 1 + 2 = 3

Question 2:

Determine the degree of unsaturation of a molecule with the molecular formula C5H4O2

Answer 2:

For CnHmOl

degree of unsaturation = (2n +2 -m)/2

n = number of C atoms = 5

m = number of H atoms = 4

degree of unsaturation = (2×5 +2 -4)/2 = 8/2 = 4

Back to the top

Problem Solving:

The Problem:

A fatty acid (long-chain carboxylic acid) has the molecular formula C18H30O2.

Determine the number of carbon-carbon double bonds in 1 molecule of this fatty acid.

Solving the Problem using the StoPGoPS model for problem solving.

STOP!

 State the question. What is the question asking you to do?

Determine the number of C=C in 1 molecule

PAUSE!

 Pause to Plan. What information have we been given?

Since this molecule is a fatty acid,
general formula is CnHmO2

What do we need to find out?

(i) Calculate degree of unsaturation = (2n +2 - m)/2

(ii) Since the C=O of the carboxyl group = 1 degree of unsaturation:
Calculate no. C=C = degree of unsaturation -1

GO!

 Go with the Plan. C18H30O2

(i) Calculate degree of unsaturation = (2n +2 - m)/2


n = 18, m = 30


degree of unsaturation = (2×18 +2 - 30)/2

= 8/2

= 4

(ii) Since the C=O of the carboxyl group = 1 degree of unsaturation:


Calculate no. C=C = degree of unsaturation -1

= 4 - 1

= 3

There are 3 C=C in this molecule.

PAUSE!

 Ponder Plausability. Have you answered the question that was asked?

Yes, we have determined the number of carbon-carbon double bonds in this molecule..

Is your solution to the question reasonable?

Work backwards


If a molecule was saturated and had a chain length of 18 carbon atoms, the maximum number of hydrogen atoms in the molecule would be 2×n +2 = 2×18 + 2 = 38 , that is, C18H38

For every one C=C bond, we remove 2 hydrogen atoms from the formula, so, for 3 C=C we remove 3×2 = 6 H atoms from the formula, that is, C18H38-6, C18H32

Addition of an O atom for the hydroxyl group (OH) makes no difference to the number of hydrogen atoms in the molecular formula: C18H32O

Addition of a double bonded oxygen to a carbon atom requires the removal of 2 hydrogen atoms from the molecular formula: C18H32-2O2, C18H30O2

Since this is the same as the molecular formula given in the question, we are reasonably confident that the fatty acid contains 3 C=C and 1 COOH functional group.

STOP!

 State the solution. There are 3 carbon-carbon double bonds in this molecule.

Back to the top

Resources for Students and Teachers

Footnotes

(1) Note that all discussions on this page refer to aliphatic organic compounds, that is, this discussion looks at non-aromatic organic compounds.
Go back to the Degree of Unsaturation: Hydrocarbons

(2) Note that an aliphatic ring is considered saturated if it contains no double nor triple bonds.
An aliphatic ring is considered unsaturated if it contains either double or triple bonds.
Go back to the Degree of Unsaturation: Hydrocarbons

(3) Note that butanal would be considered an example of a saturated aldehyde, or an alkanal, since it contains no C=C nor C≡C
Go back to the Degree of Unsaturation: Oxidised Hydrocarbons

(4) Note that butanoic acid would be considered an example of a saturated carboxylic acid, or an alkanoic acid, since it contains no C=C nor C≡C
Go back to the Degree of Unsaturation: Oxidised Hydrocarbons

Back to the top