Precipitation Conductometric Titrations Chemistry Tutorial

Key Concepts

• A precipitate is an insoluble solid that forms when solutions are mixed.
• The formation of a precipitate removes ions from electrolytic solutions.
• In a precipitation titration, one electrolyte is gradually added to another and a precipitate forms.
• If the electrical conductivity of the solution is recorded during the titration we refer to this as a conductometric precipitation titration (or precipitation conductometric titration).
• Whether or not the conductance of a solution decreases as the precipitate forms will depend on the relative mobility of the ions in solution.
• Past the end point of the precipitation titration, the conductance of the solution increases as the concentration of ions in solution increases.
• The end point⁽¹⁾ of the precipitation titration is indicated by the change in slope of the conductance curve (the intersection of 2 straight lines).
• Precipitation conductometric titrations can be used to determine the concentration of an electrolytic solution.

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Mobility of Ions and Conductivity

Some ions are more mobile than others and hence produce solutions that are better conductors of an electric current.
The conductance of a number of different cations and anions is given in the table below⁽²⁾:

Note that hydrogen ions, H⁺_(aq) (protons or hydrons), and hydroxide ions, OH^-_(aq) have the highest values for conductance and therefore will produce solutions with the highest conductivity.

Also note the similarity in the conductance of nitrate ions, NO₃^-_(aq), and halide ions (Cl^-_(aq), Br^-_(aq), I^-_(aq)).

If we are interested in the precipitation of an insoluble halide such as silver chloride (AgCl_(aq)), then we could use a solution of silver nitrate (AgNO_3(aq)) since all nitrates are soluble.
But what reagent would we use for the source of halide ions, in this case chloride ions (Cl^-_(aq))?
We can't use a hydrohalic acid such as hydrochlorice acid (HCl_(aq)) because, although it is a good source of chloride ions, the conductance of the solution will be so high due to the presence of highly mobile H⁺_(aq) that it will mask any changes in conductivity due to the precipitation reaction.
Better choices for the source of halide ions are the soluble salts of Group 1 metals since the salts of Group 1 elements are soluble, such as potassium chloride (KCl_(aq)).

Worked Example: Precipitation Titration of KCl_(aq) with AgNO_3(aq)

Potassium chloride, KCl_(aq), is a strong electrolyte, it dissociates completely into potassium cations, K⁺_(aq), and chloride anions, Cl^-_(aq), according to the following balanced chemical equation:

KCl_(aq) → K⁺_(aq) + Cl^-_(aq)

Therefore an aqueous solution of potassium chloride contains only the ions K⁺_(aq) and Cl^-_(aq).
The solution does not contain any undissociated KCl "molecules", and will be a good conductor of electricity.

Silver nitrate, AgNO_3(aq), is also a strong electrolyte, it dissociates completely in water to produce silver cations, Ag⁺_(aq), and nitrate anions, NO₃^-_(aq), according to the following balanced chemical equation:

AgNO_3(aq) → Ag⁺_(aq) + NO₃^-_(aq)

Therefore an aqueous solution of silver nitrate contains only the ions Ag⁺_(aq) and NO₃^-_(aq).
The solution does not contain any undissociated AgNO_3(aq) "molecules", and will be a good conductor of electricity.

Silver chloride, AgCl_(s), is insoluble in water, so when we add AgNO_3(aq) to KCl_(aq) a white precipitate of AgCl_(s) forms.
We can represent this precipitation reaction by a net ionic equation as shown below:

Ag⁺_(aq) + Cl^-_(aq) → AgCl_(s)

We could set up an experiment like the one below to monitor the changes in conductivity of the solution as silver nitrate is added slowly and gradually to the aqueous solution of potassium chloride⁽⁴⁾:

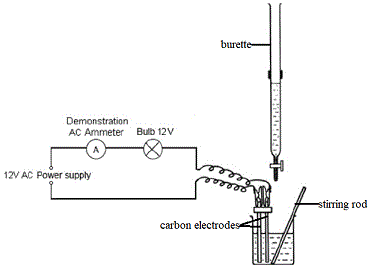Burette contains AgNO3(aq) Beaker contains KCl(aq) When conductance is high the ammeter reading will be high and the bulb will glow brightly. When conductance is low the ammeter reading will be low and the bulb will glow less brightly. Note that you may have access to a conductivity meter and data logger which would follow the changes in conductivity of the solution rather than our electrodes, ammeter and bulb arrangement.

Before any silver nitrate is added to the solution, the electrical conductivity of the potassium chloride solution is high due to the presence of potassium cations and chloride ions.

As silver nitrate is added to the beaker, a precipitate of silver chloride, AgCl_(s) starts to form:

K⁺_(aq) + Cl^-_(aq) + Ag⁺_(aq) + NO₃^-_(aq) → AgCl_(s) + K⁺_(aq) + NO₃^-_(aq)

Note that while the KCl_(aq) is in excess, the solution will also contain unreacted Cl^-_(aq).

We would expect the electrical conductivity of the solution to decrease as the silver chloride precipitate forms, effectively removing ions from the solution which should reduce the ability of the resultant solution to conduct electricity.

But this is NOT what happens!

While the KCl_(aq) is in excess, the addition of 1 AgNO_3(aq) "molecule" removes 1 Cl^-_(aq) from solution BUT it adds 1 NO₃^-_(aq) to the solution.

Let's compare the conductance of Cl^-_(aq) and NO₃^-_(aq) (see the table in the section above):

The conductance of Cl^-_(aq) and NO₃^-_(aq) is very similar, so there will be no significant change in the conductivity of the solution while KCl_(aq) is in excess.

What happens when all the available Cl^-_(aq) from the KCl_(aq) has reacted?
When the AgNO_3(aq) becomes the reactant in excess, as we add more AgNO_3(aq) to the solution, we are adding more Ag⁺_(aq) and NO₃^-_(aq) to the solution.
The concentration of ions in solution is increasing, so the conductance of the solution will also increase.

If we were to plot the conductivity of the solution as we gradually add AgNO_3(aq) we would get a conductance curve like the one shown below:

If the burette in our experiment contained 0.20 mol L^-1 AgNO_3(aq), then the conductance curve indicates that the end point of the titration occurred when 2.5 mL of this solution were added to the beaker.
We can calculate the moles of AgNO_3(aq) that was used to react completely with the KCl_(aq) in the beaker at the equivalence point:

c(AgNO_3(aq)) = [AgNO_3(aq)] = 0.20 mol L^-1

V(AgNO_3(aq)) = 2.5 mL = 2.5 mL ÷ 1000 mL/L = 0.0025 L

n(AgNO_3(aq)) = c(AgNO_3(aq)) × V(AgNO_3(aq)) = 0.20 mol L^-1 × 0.0025 L = 5.0 × 10^-4 mol

At the equivalence point the stoichiometric ratio (mole ratio) of AgNO_3(aq) to KCl_(aq) is 1:1 as shown by the balanced chemical equation below :

AgNO_3(aq) + KCl_(aq) → AgCl_(s) + NO₃^-_(aq) + K⁺_(aq)

So, at the equivalence point, 5.0 × 10^-4 mol AgNO_3(aq) reacts completely with 5.0 × 10^-4 mol KCl_(aq)

If 25.0 mL of KCl_(aq) was originally added to the beaker, then we can calculate the concentration of the KCl_(aq):

n(KCl_(aq)) = 5.0 × 10^-4 mol

V(KCl_(aq)) = 25.0 mL = 25.0 mL ÷ 1000 mL/L = 0.0250 L

c(KCl_(aq)) = n(KCl_(aq)) ÷ V(KCl_(aq)) = (5.0 × 10^-4 mol) ÷ ( 0.0250 L) = 0.020 mol L^-1

The concentration of KCl_(aq) used in the experiment was 0.020 mol L^-1

Worked Example: Precipitation Titration of Ba(OH)_2(aq) with H₂SO_4(aq)

Barium hydroxide, Ba(OH)_2(aq), is a strong electrolyte. In aqueous solution Ba(OH)_2(aq) completely dissociates into ions, barium ions, Ba²⁺_(aq), and hydroxide ions, OH^-_(aq), as shown in the balanced chemical equation below:

Ba(OH)_2(aq) → Ba²⁺_(aq) + 2OH^-_(aq)

Note that hydroxide ions, OH^-_(aq) are very mobile and therefore result in a solution that is a very good conductor of electricity.

Sulfuric acid, H₂SO_4(aq), is a strong electrolyte because it fully dissociates resulting in hydrogen ions, H⁺_(aq) (protons or hydrons), and sulfate ions, SO₄^2-_(aq), as shown by the balanced chemical equation below⁽⁵⁾:

H₂SO_4(aq) → 2H⁺_(aq) + SO₄^2-_(aq)

Note that hydrogen ions, H⁺_(aq) are very mobile and therefore result in a solution with high conductance.

When sulfuric acid is added to barium hydroxide in aqueous solution, a precipitate of barium sulfate is formed, BaSO_4(s), and water, H₂O_(l), is also produced as shown in the balanced molecular equation below:

Ba(OH)_2(aq) + H₂SO_4(aq) → BaSO_4(s) + 2H₂O_(l)

Initially, as sulfuric acid is added to excess barium hydroxide, ions are being removed from the solution in order to form both the precipitate and water molecules, so we expect the conductivity of the solution to decrease.
Past the equivalence point, when all the barium hydroxide in solution has already reacted, the further addition of sulfuric acid results in increased concentration of hydrogen ions and sulfate ions in solution so the conductivity of the solution should increase.

We could set up an experiment like the one below to monitor the changes in conductivity of the solution as sulfuric acid is added slowly and gradually to the aqueous solution of barium hydroxide:

Burette contains 1.0 mol L-1 H2SO4(aq) Beaker contains 50.0 mL Ba(OH)2(aq) When conductance is high the ammeter reading will be high and the bulb will glow brightly. When conductance is low the ammeter reading will be low and the bulb will glow less brightly. Note that you may have access to a conductivity meter and data logger which would follow the changes in conductivity of the solution rather than our electrodes, ammeter and bulb arrangement.

If you draw a graph of the results of the experiment, they will probably look like the conductance curve given below:

From the graph we see that 5.0 mL of 1.0 mol L^-1 H₂SO_4(aq) was needed to react completely with 50.0 mL of the Ba(OH)_2(aq) present in the beaker.
We can use this information to calculate the moles of H₂SO_4(aq) used to react completely with theBa(OH)_2(aq):

c(H₂SO_4(aq)) = 1.0 mol L^-1

V(H₂SO_4(aq)) = 5.0 mL = 5.0 mL ÷ 1000 mL/L = 0.0050 L

n(H₂SO_4(aq)) = c(H₂SO_4(aq)) × V(H₂SO_4(aq)) = 1.0 mol L^-1 × 0.0050 L = 5.0 × 10^-3 mol

From the balanced chemical equation we see that the stoichiometric ratio (mole ratio) of Ba(OH)_2(aq) : H₂SO_4(aq) is 1:1

Ba(OH)_2(aq) + H₂SO_4(aq) → BaSO_4(s) + 2H₂O_(l)

Therefore we calculate the moles of Ba(OH)_2(aq):

n(Ba(OH)_2(aq)) = n(H₂SO_4(aq)) = 5.0 × 10^-3 mol

Using this information we can calculate the concentration of Ba(OH)_2(aq) in the beaker:

n(Ba(OH)_2(aq)) = 5.0 × 10^-3 mol

V(Ba(OH)_2(aq)) = 50.0 mL = 50.0 mL ÷ 1000 mL/L = 0.050 L

c(Ba(OH)_2(aq)) = n(Ba(OH)_2(aq)) ÷ V(Ba(OH)_2(aq)) = (5.0 × 10^-3 mol) ÷ 0.050 L = 0.10 mol L^-1

The concentration of Ba(OH)_2(aq) used in the experiment was 0.10 mol L^-1