Capillary Action

Key Concepts

• Capillary action is also known as capillarity, capillary motion, or wicking.
• Capillary action is defined as the movement of a fluid within a capillary, a narrow tube, due to the forces of cohesion and adhesion.
• Capillary action is responsible for the formation of the meniscus observed when a fluid is present in a tube.
• The shape of the meniscus is determined by the relative strengths of the cohesive and adhesive forces:

  relative strength		Meniscus Shape
  cohesion	adhesion
  strong	weak	convex (curved up: ∩)
  weak	strong	concave (curved down: ∪)

• Whether a fluid in a capillary suspended in a reservoir of fluid rises above or falls below the level of fluid in the reservoir depends on the relative strengths of the cohesive and adhesive forces.

  relative strength		Observation
  cohesion	adhesion
  strong	weak	fluid falls
  weak	strong	fluid rises

• How far a fluid in a capillary rises above, or falls below, the level of fluid in the reservoir depends on the diameter of the capillary.

  The smaller the diameter of the capillary, the greater the movement of the fluid.

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Observing Capillary Action

You have been observing capillary action your whole life. Every time you place a drinking straw into a fluid such as water, cordial, fruit juice, or fizzy drink, you will have noticed that the fluid rises up the straw as soon as the straw makes contact with the fluid, just like the diagram on the right. In the science laboratory you have probably placed a celery stalk in coloured water and watched as the coloured water rises up the capillaries in the celery. And you have probably also undertaken a paper chromatography experiment in which you placed a spot of black ink on filter paper suspended in water and watched the black spot rise up the paper and separate into different colours. Have you ever stopped to think how odd this is? Gravity is a force that pulls things down. If you turn on the water tap, water falls down from the tap, not up. Melting snow on a mountain streams down the mountain, not up. The forces that allow water to rise up the straw, celery stalk or filter paper, must be strong enough to overcome gravity. These forces are known as cohesion and adhesion.

Cohesion

These stronger intermolecular forces of attraction will be either:

• hydrogen bonds
  (for polar molecules in which H is covalently bonded to F, O or N in the molecule)
• dipole-dipole interactions
  (any other polar molecule)

The stronger the intermolecular forces of attraction acting between the particles in the liquid, the stronger the cohesive force holding the particles together.

Adhesion

The strength of the adhesive force (adhesion) between molecules in the liquid and molecules in the solid will therefore depend on the nature of the molecules making up the liquid and the solid.

The more similar the molecules in the liquid and the molecules in the solid are, the stronger the adhesive force is likely to be.
For example, water molecules are polar and the surface of silica glass is polar so the force of adhesion between water and silica is likely to be quite strong.
Water is polar but paraffin wax is non-polar, so the force of adhesion between water and wax is likely to be quite weak.
Hexane is non-polar and paraffin wax is non-polar, so the force of adhesion between hexane and wax is likely to be quite strong.

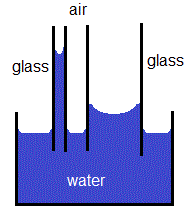
Shape of a Meniscus

Water can wet the surface of glass because the adhesive force of attraction between water molecules and the glass surface is greater than the cohesive forces of attraction between the water molecules.

If a silica glass tube is positioned vertically in a reservoir of water, the same forces of adhesion and cohesion are at work.
In the representation below, we are looking at a cross-section of water molecules inside a silica glass capillary tube:

Because the forces of adhesion are greater than the forces of cohesion, the water molecules prefer to make hydrogen bonds with the silica glass rather than with other water molecules.
This causes the water molecules close to the silica glass to creep up the glass, wetting more of the glass.
At the same time, the forces of attraction between water molecules at the boundary between water and air are unbalanced, so the water molecules at this surface are experiencing a pull towards the body of the liquid water (surface tension).
The result of both of these forces, cohesion and adhesion, is the formation of the familiar concave mensicus shape for water in a capillary tube.

Compared to water molecules in liquid water, mercury has much stronger intermolecular forces of attraction acting between the mercury atoms, metallic bonds, so the cohesive force for mercury is much stronger than the cohesive force for water.
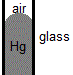If mercury is placed in a silica glass capillary tube, the force of cohesion between mercury atoms is greater than the force of adhesion between mercury atoms and the silica glass.
Mercury atoms therefore "pull away" from the silica glass surface, wetting less of the glass, while the cohesive forces of attraction between the mercury atoms at the boundary between mercury and air are unbalanced and pull the mercury atoms towards the body of the liquid mercury.
This results in the formation of the familiar convex mensicus for mercury in a glass capillary tube.

To summarise:

• cohesion > adhesion → convex meniscus
• cohesion < adhesion → concave meniscus

The shape of the meniscus has important implications when measuring the volume of liquids.
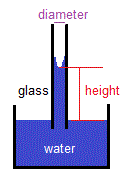
You will have been taught to always measure the volume of liquid in a measuring cylinder, burette, pipette, etc, by reading from the bottom of the meniscus when viewed at eye level.
Why?
Because the glassware you use has been calibrated to measure volumes of water, taking into account the shape, and hence the volume, of the meniscus.
This means that if you measure the volume of water in the apparatus above the bottom of the meniscus, you will be overstating the volume of water. If you measure the volume of water in the apparatus below the bottom of the meniscus, you will be understating the volume of water.
What happens if you use your apparatus to measure the volume of a liquid other than water?
The truth is that your measurement will only be approximate, because the shape of the meniscus, and hence its volume, will be different to that of water. You could re-calibrate the apparatus specifically to measure volumes of a different liquid if you need a more accurate measurement.

Height of a Column of Liquid in a Capillary Tube

A pasteur pipette is an open-ended silica glass tube. Observe that one end of a pasteur pipette is a capillary tube with a larger diameter than the other end. Place a pasteur pipette in a reservoir of water so that the larger diameter capillary tube is suspended in the reservoir of water. Place another pasteur pipette with the smaller diameter capillary tube suspended in the same reservoir of water. You should see that the water level in the smaller diameter capillary tube is higher than the water level in the larger diameter capillary tube, as shown in the diagram on the right. smaller diameter glass capillary tube → higher height of column of water in tube larger diameter glass capillary tube → lower height of column of water in tube

You can perform your own experiments using a number of open-ended glass tubes (capillary tubes) of different internal diameters.

The diameter is the internal diameter of the tube and will be measured in millimetres (mm). The height of the column of water in the capillary tube is measured from the level of the water in the reservoir to the bottom of the meniscus of the water in the capillary tube, in millimetres (mm). Enter the diameter of your capillary tube into the calculator on the right to predict the approximate height of the column of water.

water in a glass capillary tube at 20oC diameter =mm Click: height ≈mm Click: