Calorimetry Chemistry Tutorial

Key Concepts

• An calorimeter is a device used to measure the enthalpy change of a chemical reaction (heat of reaction).
• An adiabatic calorimeter¹ is designed to minimize the transfer of heat between the reaction vessel and its surroundings.
• A calorimeter can be used to determine the enthalpy change for a chemical reaction (heat of reaction), by measuring the:

  (a) input of electrical energy

  (b) resultant increase in temperature

• The two types of calorimeters to be discussed below are:

  (a) Bomb Calorimeter: measure heat of combustion (enthalpy of combustion)

  (b) Solution Calorimeter: measure heat of solution, heat of neutralisation, etc

Please do not block ads on this website.
No ads = no money for us = no free stuff for you!

Bomb Calorimeter

A bomb calorimeter is used to measure enthalpy of combustion (heat of combustion).

A combustion reaction is always exothermic (reaction releases energy).

A bomb calorimeter can be used to measure heat content of foods and fuels.

A schematic diagram of a typical bomb calorimeter is shown below:

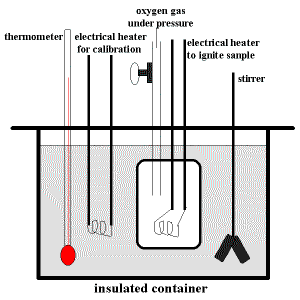
The "bomb" is the inner steel container in which the sample will be combusted rapidly and completely using oxygen gas at a pressure of about 25 atm (≈ 2533 kPa).
An electrical heater inside the "bomb" is used to ignite the sample.

The "bomb" is immersed in a can of water fitted with a thermometer and a stirrer.
The stirrer will circulate the water to ensure that the temperature of the water in different places within the container will be the same.
The thermometer is used to record the intial temperature which is the temperature before the combustion reaction, and, the final temperature which is the maximum temperature reached after the combustion reaction.

You will also notice an item labelled "electrical heater for calibration" inside the can of water.
Before a sample is combusted in the "bomb", the calorimeter must be calibrated to determine how much energy must be supplied to increase the temperature of the water by 1°C.

Calibration of the Bomb Calorimeter

Electrical energy is supplied to the water in the can for a known time and the temperature change is recorded.
The calibration factor, C.F., is then calculated for this calorimeter.

• The initial temperature of the water in the can is recorded in °C

  T_i = intial temperature

• Electrical energy, E, is supplied to heat the water in the can.
      Electrical energy, E, in joules, J, can be calculated² given:
      (a) voltage, V, measured in volts, V
      (b) current, I, measured in amps, A
      (c) time, t, measured in seconds, s

  E = V × I × t

• The temperature of the water in the can increases and will reach a maximum value.
  The maximum value is recorded in °C and is called the final temperature

  T_f = final temperature

• The change in the temperature of the water in the can, ΔT, is calculated:

  ΔT = T_f - T_i

• The calibration factor, C.F., or the energy required to raise the temperature of the water in the can by 1°C is then calculated:

  C.F. = E ÷ ΔT

This calibration factor, C.F., can then be used in the next stage of the experiment to determine the heat of combustion (enthalpy of combustion) of a sample.

Using the Calibration Factor to Determine the Heat of Combustion of a Substance

Once the calorimeter has been calibrated, we can now use it to determine the heat of combustion (enthalpy of combustion) of a sample.

• A small amount of the sample (≈ 1 g) is placed in the "bomb" and the mass of the sample recorded.

  m = mass of sample in grams

• The intial temperature of the water is measured and recorded in °C before the combustion reaction takes place

  T_i = initial temperature in °C

• The sample in the bomb is ignited using electrical heater.
• The temperature of the water increases until it reaches a maximum value, the final temperature, measured in °C:

  T_f = final temperature in °C

• Then we can calculate the change in the water temperature in °C as a result of combusting the sample:

  ΔT = T_f - T_i (in °C)

• We can use this temperature change to determine the energy released by the combustion reaction using the calibration factor, C.F., calculated above:

  C.F. = E ÷ ΔT

  which can be rearranged by multiplying both sides of the equation by ΔT to give:

  E = C.F. × ΔT

  That is, the energy liberated by combustion equals the calibration factor times the change in temperature caused by the reaction.

• E is the energy released by the mass of sample, m, that was used in the experiment.
  We can therefore calculate the amount of energy released per gram of sample by dividing E by the mass, m

  E ÷ m = J g^-1

• We can also calculate the energy released per mole of sample since:

  moles = mass ÷ molar mass

  n = m ÷ M_r
  n = moles of substance
  m = mass of substance in grams
  M_r = molar mass of substance in g mol^-1

  So, E divided by the amount of sample in moles gives us the molar heat of combustion (or molar enthalpy of combustion) for this sample:

  ΔH_c = E ÷ n (in J mol^-1)

  Note, the molar heat of combustion is always given as a positive number, BUT the combustion reaction is exothermic, that is, it releases heat so the enthalpy change for the reaction is actually negative.

Worked Example: Bomb Calorimeter to Determine Heat of Combustion

Question : In an experiment to determine the energy content of naphthalene, C₁₀H₈, a bomb calorimeter was used.

Initially a constant current of 1.80 A was passed through the electric heater for 75.00 seconds. The potential difference was 4.95 V. The temperature increased from 18.25°C to 18.32°C.

A 1.19 g sample of naphthalene was then burnt in the bomb calorimeter and the temperature increased from 18.32°C to 23.74°C.

Calculate the molar heat of combustion for naphthalene in kJ mol^-1.

Solution:

(Based on the StoPGoPS approach to problem solving.)

1. What is the question asking you to do?

   Determine the heat of combustion for naphthalene in kJ mol^-1
   molar heat of combustion = kJ mol^-1

2. What data (information) have you been given in the question?

   Extract the data from the question:

   Calibration Data:
   I = current in amps = 1.80 A
   V = voltage in volts = 4.95 V
   t = time in seconds = 75.00 s
   T_i = initial temperature = 18.25°C
   T_f = final temperature = 18.32°C

   Combustion of Sample Data:
   name of sample: naphthalene
   molecular formula of naphthalene: C₁₀H₈
   m = mass of naphthalene in grams = 1.19 g
   T_a = initial temperature = 18.32°C
   T_b = final temperature = 23.74°C

3. What is the relationship between what you know and what you need to find out?

   (a) Calculate the calibration factor, C.F., for this calorimeter:

   (i) E = V × I × t

   (ii) C.F. = E ÷ (T_f - T_i)

   (b) Use the calibration factor to calculate the energy released by combustion of 1.19 g of naphthalene:

   E = C.F. × (T_b - T_a)

   (c) Calculate moles of naphthalene, C₁₀H₈:

   n = m ÷ M_r

   (d) Calculate molar heat of combustion of naphthalene:

   molar heat of combustion = E ÷ n

4. Perform the calculations

   (a) Calculate the calibration factor, C.F., for this calorimeter:

   (i) E = V × I × t

   E = 4.95 × 1.80 × 75.00 = 668.25 J

   (ii) C.F. = E ÷ (T_f - T_i)

   C.F. = 668.25 ÷ (18.32 - 18.25)
               = 668.25 ÷ 0.0700
               = 9546.4 J °C^-1

   (b) Use the calibration factor to calculate the energy released by combustion of 1.19 g of naphthalene:

   E = C.F. × (T_b - T_a)

   E = 9546.4 × (23.74 - 18.32)
               = 9546.4 × 5.42
               = 51741.5 J

   (c) Calculate moles of naphthalene, C₁₀H₈:

   n = m ÷ M_r

   M_r = (10 × 12.01) + (8 × 1.008) = 120.1 + 8.064 = 128.164 g mol^-1

   n = m ÷ M_r = 1.19 ÷ 128.164 = 9.285 × 10^-3 mol

   (d) Calculate molar heat of combustion of naphthalene:

   molar heat of combustion = E ÷ n

   molar heat of combustion = 51741.5 ÷ 9.285 × 10^-3 = 5572590 J mol^-1

   Convert J mol^-1 to kJ mol^-1 by dividing by 1,000 J/kJ:

   molar heat of combustion = 5572590 ÷ 1000 = 5573 kJ mol^-1 (5.573 × 10³ kJ mol^-1)

5. Is your answer plausible?

   (a) Molar heat of combustion is always positive by definition. 5573 kJ mol^-1 is a positive number so our answer is plausible.

   (b) Work backwards using the calculated value for heat of combustion to calculate the energy released and therefore calculate the expected temperature change for the combustion of the sample:
   energy released by combustion = heat (kJ mol^-1) × moles
   = 5573 × (1.19 ÷ 128.164) = 51 kJ = 51,000 J

   Note that the energy required to raise the temperature of water during calibration, q_cal (or heat capacity of this calorimeter), is
   q_cal = m(water) ×C_g × (T_f - T_i)
   and the energy absorbed by the water during the combustion reaction, q_com, is
   q_com = m(water) ×C_g × (T_b - T_a)
   and assuming the mass of water (m(water)) and its specific heat capacity (C_g) are constant, then:
   q_cal ÷ (T_f - T_i) = m(water) ×C_g = constant
   q_com ÷ (T_b - T_a) = m(water) ×C_g =constant
   then:
   q_cal ÷ (T_f - T_i) = q_com ÷ (T_b - T_a)
   so,
   (T_b - T_a) = q_com × (T_f - T_i) ÷ q_cal
   Substitute in the values and solve for (T_b - T_a):
   (T_b - T_a) = 51,000 × (18.32 - 18.25) ÷ 668.25 = 5.3 °C
   So, given the initial temperature of the water was 18.32 °C, the final temperature of the water after combustion should be:
   T_b = T_a + 5.3 = 18.32 + 5.3 = 23.6°C
   which is very close to the final temperature given in the question as 23.74°C so we are reasonably confident that our answer is plausible.

6. State your solution to the problem "heat of combustion of naphthalene in kJ mol^-1":

   heat of combustion of naphthalene = 5.573 × 10³ kJ mol^-1

Solution Calorimeter

A solution calorimeter can be used to measure the heat of reaction (enthalpy of reaction).
A solution calorimeter can be used to determine the

• heat of solution (enthalpy of solution)
• heat of neutralisation (enthalpy of nuetralization)
• heat of precipitation (enthalpy of precipitation)

Note that the heat of reaction (enthalpy of reaction) can be either:

• positive (for an endothermic reaction)
• negative (for an exothermic reaction)

A schematic diagram of a typical solution calorimeter is shown below:

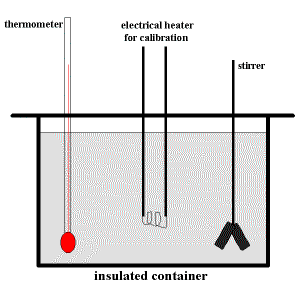
The insulated container prevents heat being lost to the surroundings and contains either

• pure solvent (if you are measuring the heat of solution of a substance)
• solution (if you measuring heat of neutralisation, heat of precipitation, etc)

The stirrer ensures thorough mixing so that the temperature of the solution, as measured by the thermometer, is the same for all locations within the calorimeter.

The electrical heater is used only during the process of calibrating the calorimeter. It is used to heat the solution (or pure solvent) in the calorimeter and determine the calibration factor, C.F., for this calorimeter.

Calibration of the Solution Calorimeter

Electrical energy is supplied to the solution (or pure solvent) in the calorimeter for a known time and the temperature change is recorded.
The calibration factor, C.F., is then calculated for this calorimeter.

• The initial temperature of the solution (or pure solvent) in the calorimeter is recorded in °C

  T_i = intial temperature

• Electrical energy, E, is supplied to heat the solution (or pure solvent) in the calorimeter.
      Electrical energy, E, in joules, J, can be calculated² given:
      (a) voltage, V, measured in volts, V
      (b) current, I, measured in amps, A
      (c) time, t, measured in seconds, s

  E = V × I × t

• The temperature of the solution (or pure solvent) in the calorimeter increases and will reach a maximum value.
  The maximum value is recorded in °C and is called the final temperature

  T_f = final temperature

• The change in the temperature of the solution (or pure solvent) in the calorimeter, ΔT, is calculated:

  ΔT = T_f - T_i

• The calibration factor, C.F., or the energy required to raise the temperature of the solution (or pure solvent) in the calorimeter by 1°C is then calculated:

  C.F. = E ÷ ΔT

This calibration factor, C.F., can then be used in the next stage of the experiment to determine the heat of reaction (enthalpy of reaction) for a chemical reaction.

Using the Calibration Factor to Determine the Heat of Reaction (enthalpy of reaction)

Once the calorimeter has been calibrated, we can now use it to determine the heat of reaction (enthalpy of reactio) of a reaction.

• The intial temperature of the solution in the calorimeter is measured and recorded in °C before the reaction takes place

  T_i = initial temperature in °C

• A known amount of reactant is added to the calorimeter.

  n = moles of reactant

• The temperature of the solution increases until it reaches a maximum value, the final temperature, measured in °C:

  T_f = final temperature in °C

• Then we can calculate the change in the solution temperature in °C as a result of the reaction:

  ΔT = T_f - T_i (in °C)

• We can use this temperature change to determine the energy released by the reaction using the calibration factor, C.F., calculated above:

  C.F. = E ÷ ΔT

  which can be rearranged by multiplying both sides of the equation by ΔT to give:

  E = C.F. × ΔT

  That is, the energy released or absorbed by the reaction equals the calibration factor times the change in temperature caused by the reaction.

• E is the energy released or absorbed by the amount of reactant, n, that was used in the experiment.
  We can therefore calculate the amount of energy released or absorbed per mole of reactant by dividing E by the moles, n

  E ÷ n = J mol^-1

  So, E divided by the amount of sample in moles gives us the molar heat of reaction (or molar enthalpy of reaction) for this sample:

  ΔH = E ÷ n (in J mol^-1)

  Note, the molar heat of reaction (molar enthalpy of reaction) can be either positive (endothermic reaction) or negative (exothermic reaction).
  If the temperature in the calorimeter increases during the reaction, the reaction is exothermic and ΔH is negative.
  If the temperature in the calorimeter decreases during the reaction, the reaction is endothermic and ΔH is positive.

Worked Example: Solution Calorimeter to Determine Heat of Solution (enthalpy of solution)

Question : A small glass ampoule containing 3.00 × 10^-3 moles of H₂SO_4(l) is placed in a calorimeter containining 100 mL of distilled water at 20.00°C.
Initially, a constant 6.00 V of electricity was applied with a current of 2.00 A passing through the electric heater for 30 seconds.
The water temperature increased to 20.77°C.
The ampoule was then broken and the maximum recorded temperature of the solution was 21.28°C.
Calculate the molar heat of solution, ΔH, in kJ mol^-1 for the reaction:
H₂SO_4(l) → H₂SO_4(aq)

Solution:

(Based on the StoPGoPS approach to problem solving.)

1. What is the question asking you to do?

   Determine the heat of solution for sulfuric acid in kJ mol^-1
   ΔH_soln = kJ mol^-1

2. What data (information) have you been given in the question?

   Extract the data from the question:

   Calibration Data:
   I = current in amps = 2.00 A
   V = voltage in volts = 6.00 V
   t = time in seconds = 30 s
   T_i = initial temperature = 20.00°C
   T_f = final temperature = 20.77°C

   Dissolving Sulfuric Acid in Water Data:
   name of solute: sulfuric acid
   n = moles of sulfuric acid in mol = 3.00 × 10^-3 mol
   T_a = initial temperature = 20.77°C (temperature of water when ampoule was broken)
   T_b = final temperature = 21.28°C

3. What is the relationship between what you know and what you need to find out?

   (a) Calculate the calibration factor, C.F., for this calorimeter:

   (i) E = V × I × t

   (ii) C.F. = E ÷ (T_f - T_i)

   (b) Use the calibration factor to calculate the energy released by dissolving sulfuric acid in water:

   E = C.F. × (T_b - T_a)

   (c) Calculate molar heat of solution of sulfuric acid:

   ΔH_soln = E ÷ n

4. Perform the calculations

   (a) Calculate the calibration factor, C.F., for this calorimeter:

   (i) E = V × I × t

   E = 6.00 × 2.00 × 30 = 360 J

   (ii) C.F. = E ÷ (T_f - T_i)

   C.F. = 360 ÷ (20.77 - 20.00)
               = 360 ÷ 0.77
               = 467.5 J °C^-1

   (b) Use the calibration factor to calculate the energy released by dissolving sulfuric acid in water:

   E = C.F. × (T_b - T_a)

   E = 467.5 × (21.28 - 20.77)
               = 467.5 × 0.51
               = 238.4 J

   (c) Calculate molar heat of solution of sulfuric acid:

   molar heat of solution = -E ÷ n
   (reaction is exothermic because temperature increased, ΔH is negative)

   ΔH_soln = -238.4 ÷ 3.00 × 10^-3 = -79467 J mol^-1

   Convert J mol^-1 to kJ mol^-1 by dividing by 1,000 J/kJ:

   ΔH_soln = -79467 ÷ 1000 = -79.5 kJ mol^-1 (-7.95 × 10¹ kJ mol^-1)

5. Is your answer plausible?

   Do an approximate calculation of the heat of solution based on the heat released when H₂SO_4(l) dissolves in 100 mL of water using the mass and specific heat capacity of weater:
   q = m × C_g × (T_b - T_a)
   q = energy released in J
   m = mass of solution approximated as mass of water = 100 g
   (assuming density of solution is 1.00 g mL^-1 and mass of H₂SO_4(l) is negligible.)
   C_g = heat capacity of solution ≈ heat capacity of water ≈ 4.2 J g^-1 °C^-1
   T_b - T_a = 21.28 - 20.77 = 0.51°C
   q = 100 × 4.2 × 0.51 = 214.2 J

   ΔH_soln = -q ÷ n = -214.2 ÷ 3.00 × 10^-3 = -71400 J = -71.4 kJ

   Since the results of the "rough" calculation are about the same as that calculated using the more accurate calibration factor (-71.4 kJ is close to -79.5 kJ) we are reasonably confident that our answer is correct.

6. State your solution to the problem "heat of solution in kJ mol^-1":

   ΔH_soln = -79.5 kJ mol^-1

Footnotes